Затухающие колебания физического маятника

Сила сопротивления движению шара в воздухе направлена противоположно его скорости и зависит от сложным образом ([8], см. работу № 1.6). При медленном движении шара диаметром сила сопротивления пропорциональная скорости

, (8.23)

где - динамическая вязкость воздуха, 18,1 мкПа×с. Применимость этой формулы Стокса ограничена значениями числа Рейнольдса

. (8.24)

При более точном рассмотрении движения жидкости вдали от шарика К. Осееном было получено следующее выражение для силы, применимое при

. (8.25)

При колебаниях маятника шар движется с переменной скоростью, поэтому при вычислении числа Рейнольдса в качестве скорости можно использовать среднее за полупериод, в течение которого шар движется в одном направлении

,(8.26)

где - амплитуда линейных смещений математического маятника. Для уменьшения значений в данной работе необходимо использовать возможно большую длину нити и возможно меньший диаметр .

Скорость движения шара (сферы) на нити, (см. рис. 8.1),) связана с угловой скоростью

, (8.27)

где вектор направлен из точки подвеса в центр сферы. Сила сопротивления направлена противоположно вектору скорости , поэтому ее момент относительно оси вращения

. (8.28)

С использованием математической формулы для двойного векторного произведения

, (8.29)

и перпендикулярности векторов и получим выражения для вектора момента сил сопротивления

. (8.30)

и проекции этого момента на ось

. (8.31)

С учетом сопротивления воздуха уравнение (8.5) изменится

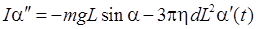, (8.32)

или для малых углов уравнение

, (8.33)

. (8.34)

Это уравнение является примером общего уравнения свободных затухающих колебаний

, (8.35)

со значениями параметров

, , (8.36)

для математического маятника с длиной нити

, .. (8.37)

Решения уравнения (8.46) в случае слабого затухания, представляют собой затухающие колебания

, (8.38)

с циклической частотой

, (8.39)

периодом

, (8.40)

и убывающей по экспоненциальному закону амплитудой

. (8.41)

Затухающие колебания характеризуют следующие величины:

1) время релаксации и время уменьшения амплитуды вдвое

, ; (8.42)

2) декремент затухания – отношения амплитуд двух последовательных колебаний, соответствующих моментам времени, отличающимся на период

; (8.43)

3) логарифмический декремент затухания

, (8.44)

где - число колебаний, совершаемых за время уменьшения амплитуды в раз, которое можно выразить через число колебаний, совершаемых за время уменьшения амплитуды вдвое