Математическая статистика

Вопросы к зачету по дисциплине «Статистические методы в металлургии»

1. Предмет и основные задачи математической статистики.

2. Генеральная совокупность и выборка, репрезентативность выборки.

3. Основные понятия математической статистики (вариационный ряд, частота, относительная частота, статистическое распределение выборки).

4. Построение эмпирической функции распределения выборки.

5. Построение полигона и гистограммы относительных частот. Формула Старджеса.

1. Точечные оценки неизвестных параметров распределения и их свойства.
2. Выборочная средняя. Выборочная и исправленная дисперсии. Эмпирические моменты.

8. Интервальные оценки параметров распределения. Понятия надежности оценки доверительного интервала.

1. Построение доверительного интервала для математического ожидания при известном среднеквадратическом отклонении.
2. Построение доверительного интервала для оценки генеральной средней при неизвестном среднеквадратическом отклонении.

11. Построение доверительного интервала для оценки среднего квадратического отклонения.

1. Основные понятия теории проверки статистических гипотез. Критерии согласия. Уровень значимости. Ошибки первого и второго рода.

13. Критерий Пирсона проверки гипотезы о нормальном распределении генеральной совокупности.

14. Методика расчета теоретических частот при применении критерия Пирсона.

15. Критерий Колмогорова проверки гипотезы о виде закона распределения.

1. Элементы корреляционного анализа. Корреляционная таблица. Условные средние.
2. Выборочный коэффициент корреляции и его свойства.

18. Уравнение выборочной регрессии.

19. Выборочный коэффициент регрессии. Связь между выборочными коэффициентами регрессии корреляции.

20. Построение линейной регрессии методом наименьших квадратов.

 

 

Задачи для подготовки к зачету

Математическая статистика

• Найти доверительный интервал для оценки с надежностью 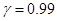неизвестного математического ожидания нормально распределенного признака генеральной совокупности , если известны объем выборки выборочная средняя среднее квадратическое отклонение генеральной совокупности .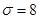

· Найти исправленную выборочную дисперсию по данному распределению выборки объема :

	-2

 

• По выборке объема 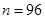построена гистограмма частот.

Найти значение .

 

· В результате измерений некоторой случайной величины одним прибором (без систематических ошибок) получены следующие результаты: 5, 7, 4, 3, 6 мм. Определить несмещенную оценку дисперсии измерений

 

· Для выборки объема n =100, представленной вариационным рядом, построить полигон относительных частот и гистограмму частот.

 

По выборке объема , найдена смещенная оценка генеральной дисперсии. Найти несмещенную оценку дисперсии.

 

· В таблице представлены эмпирические частоты и теоретические частоты , которые вычислены исходя из гипотезы о нормальном распределении генеральной совокупности. Используя критерий Пирсона, при уровне значимости 0,05 проверить гипотезу о нормальности закона распределения генеральной совокупности.

 

• Из генеральной совокупности извлечена выборка:

Найти несмещенные оценки генеральной средней и генеральной дисперсии.

 

• Найти доверительный интервал для оценки с надежностью 0,95 неизвестного математического ожидания нормально распределенного признака генеральной совокупности, если известны генеральное среднее квадратическое отклонение , выборочная средняя и объем выборки .

 

• По данным 16 независимых равноточных измерений некоторой физической величины найдены среднее арифметическое результатов измерений и «исправленное» среднее квадратическое отклонение . Оценить истинное значение измеряемой величины с помощью доверительного интервала с надежностью 0,99. Предполагается, что результаты измерений распределены нормально.

 

• По выборке двумерной генеральной совокупности, представленной таблицей, найти выборочный коэффициент корреляции:

 

X Y	-3

Образец билета

министерство образования и науки российской федерации

федеральное государственное бюджетное образовательное учреждение высшего образования

«МОСКОВСКИЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»

(МОСКОВСКИЙ ПОЛИТЕХ)

Факультет базовых компетенций, центр математического образования

Дисциплина «Статистические методы в металлургии»

Образовательная программа 22.03.02 Металлургия

Курс 4, семестр 7

БИЛЕТ №

1. Критерий Пирсона проверки гипотезы о нормальном распределении генеральной совокупности.

2. Из генеральной совокупности извлечена выборка малого объема:

 

	-2

 

Построить доверительный интервал, в котором с надежностью будет заключено математическое ожидание нормально распределенного признака X генеральной совокупности.

 

Утверждено на заседании ЦМО

И.о. заведующего центром /Г.С. Жукова /

_______________________________________________________________________________________

 

 

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

ВЫСШЕГО ОБРАЗОВАНИЯ

«МОСКОВСКИЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»

(МОСКОВСКИЙ ПОЛИТЕХ)

Факультет базовых компетенций, центр математического образования Дисциплина «Статистические методы в металлургии» Образовательная программа 22.03.02 Металлургия Курс 4, семестр 7

БИЛЕТ №

 

1. Коэффициент корреляции и его свойства.

1. Для статистического распределения выборки

 

 

Найти выборочную среднюю и исправленную дисперсию .

 

Утверждено на заседании ЦМО

И.о. заведующего центром/Г.С. Жукова /