Лабораторная работа ЭМК-3 К. Изучение поляризации диэлектрика и определение емкости конденсатора
Цель работы: изучение поляризации диэлектрика и определение электрофизических свойств конденсатора.
Задачи:
- градуировка баллистического гальванометра и определение емкости конденсатора в зависимости от его геометрических параметров;
- изучение электрофизических свойств конденсатора при неизменном напряжении на его обкладках;
- изучение электрофизических свойств конденсатора при его неизменном заряде.
Метод измерения емкости 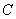 конденсатора основан на зарядке конденсатора до известного значения напряжения
конденсатора основан на зарядке конденсатора до известного значения напряжения 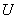 , измерении его заряда
, измерении его заряда 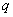 и вычислении по формуле
и вычислении по формуле
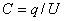 . (2.1)
. (2.1)
Заряд конденсатора измеряется c помощью зеркального гальванометра, работающего в баллистическом режиме (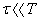 ). Здесь
). Здесь 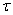 - длительность импульса тока, проходящего через гальванометр,
- длительность импульса тока, проходящего через гальванометр, 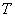 - период собственных колебаний гальванометра. В таком режиме максимальный отброс
- период собственных колебаний гальванометра. В таком режиме максимальный отброс 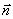 светового «зайчика» по шкале прибора будет пропорционален заряду
светового «зайчика» по шкале прибора будет пропорционален заряду 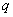 . До начала измерений заряда с помощью баллистического гальванометра последний нужно проградуировать, используя конденсатор известной емкости
. До начала измерений заряда с помощью баллистического гальванометра последний нужно проградуировать, используя конденсатор известной емкости 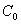 , т.е. снять зависимость
, т.е. снять зависимость 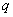 от
от 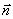 .
.
Емкость 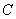 плоского конденсатора равна
плоского конденсатора равна
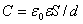 , (2.2)
, (2.2)
где 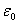 - электрическая постоянная;
- электрическая постоянная;
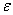 - диэлектрическая проницаемость среды;
- диэлектрическая проницаемость среды;
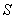 - площадь обкладки;
- площадь обкладки;
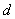 - расстояние между обкладками (пластинами) конденсатора.
- расстояние между обкладками (пластинами) конденсатора.
Электрическое поле плоского конденсатора является однородным 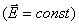 и при отсутствии диэлектрика (для воздуха
и при отсутствии диэлектрика (для воздуха 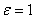 ) характеризуется напряженностью
) характеризуется напряженностью 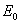 поля сторонних зарядов [1]
поля сторонних зарядов [1] 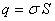
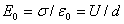 (2.3)
(2.3)
и электрическим смещением (или электрической индукцией)
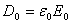 , (2.4)
, (2.4)
где 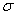 - поверхностная плотность сторонних зарядов
- поверхностная плотность сторонних зарядов 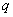 .
.
Поле вектора 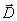 можно изображать с помощью силовых линий, которые начинаются и кончаются лишь на сторонних зарядах. Как видно из (2.4), направления
можно изображать с помощью силовых линий, которые начинаются и кончаются лишь на сторонних зарядах. Как видно из (2.4), направления 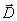 и
и 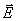 совпадают.
совпадают.
При заполнении пространства между обкладками диэлектриком с проницаемостью 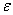 свойства конденсатора изменяются. Под действием поля диэлектрик поляризуется: дипольные моменты молекул вещества ориентируются в направлении поля и на противоположных сторонах диэлектрика (см. рис. 2.1) появляются связанные заряды
свойства конденсатора изменяются. Под действием поля диэлектрик поляризуется: дипольные моменты молекул вещества ориентируются в направлении поля и на противоположных сторонах диэлектрика (см. рис. 2.1) появляются связанные заряды 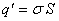 . Эти заряды создадут внутри диэлектрика однородное поле, напряженность которого равна
. Эти заряды создадут внутри диэлектрика однородное поле, напряженность которого равна 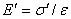 . Вне диэлектрика
. Вне диэлектрика 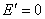 . Оба поля
. Оба поля 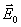 и
и 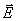 направлены навстречу друг другу и, следовательно, в пространстве между обкладками конденсатора напряженность результирующего поля равна
направлены навстречу друг другу и, следовательно, в пространстве между обкладками конденсатора напряженность результирующего поля равна
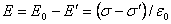 . (2.5)
. (2.5)
Вне диэлектрика 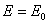 .
.
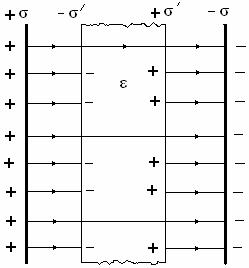
Рисунок 2.1
Так как поверхностная плотность связанных зарядов 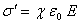 , то, подставив это значение в формулу (2.5), получим
, то, подставив это значение в формулу (2.5), получим
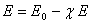 ,
,
откуда
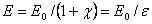 , (2.6)
, (2.6)
т.е. диэлектрическая проницаемость 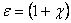 показывает, во сколько раз ослабляется поле в диэлектрике по сравнению с вакуумом, поэтому густота силовых линий
показывает, во сколько раз ослабляется поле в диэлектрике по сравнению с вакуумом, поэтому густота силовых линий 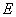 в диэлектрике в
в диэлектрике в 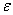 раз меньше, чем в вакууме.
раз меньше, чем в вакууме.
Для понимания явления поляризации диэлектрика и выяснения физического смысла величин 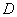 и
и 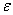 , рассмотрим два примера полей в конденсаторе.
, рассмотрим два примера полей в конденсаторе.
Пример 1. При введении диэлектрика в зазор напряжение между обкладками остается неизменным (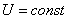 , источник не отключен от конденсатора):
, источник не отключен от конденсатора):
а) пусть диэлектрик полностью заполняет пространство между обкладками конденсатора. Вследствие поляризации диэлектрика емкость конденсатора увеличивается в 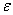 раз, т.е.
раз, т.е. 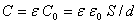 и, следовательно, увеличиваются заряды на обкладках конденсатора. Однако приращение сторонних зарядов
и, следовательно, увеличиваются заряды на обкладках конденсатора. Однако приращение сторонних зарядов 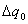 компенсируется появлением связанных зарядов
компенсируется появлением связанных зарядов 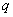 , и поэтому напряженность поля
, и поэтому напряженность поля 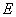 остается неизменной
остается неизменной
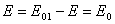 , (2.7)
, (2.7)
где 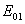 - поле сторонних зарядов
- поле сторонних зарядов 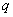 ;
;
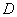 - электрическое смещение поля.
- электрическое смещение поля.
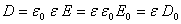 , (2.8)
, (2.8)
т.е. значение вектора электрического смещения 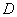 увеличивается в
увеличивается в 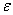 раз, т.к. источниками линий
раз, т.к. источниками линий 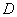 являются сторонние заряды
являются сторонние заряды 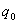 ;
;
б) пусть диэлектрик заполняет только вторую половину зазора (рис. 2.2). Емкость конденсатора 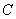 вследствие поляризации диэлектрика уменьшается и определяется равенством
вследствие поляризации диэлектрика уменьшается и определяется равенством
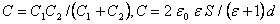 , (2.9)
, (2.9)
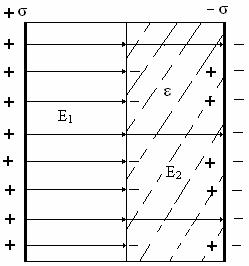
Рисунок 2.2
где 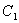 - емкость воздушной половины зазора;
- емкость воздушной половины зазора;
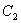 - емкость второй половины зазора с диэлектриком
- емкость второй половины зазора с диэлектриком 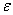 .
.
С увеличением за счет источника сторонних зарядов 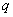 на обкладках и появления связанных зарядов
на обкладках и появления связанных зарядов 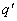 на диэлектрике электрическое поле в первой (воздушной) половине зазора характеризуется напряженностью
на диэлектрике электрическое поле в первой (воздушной) половине зазора характеризуется напряженностью 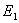 и смещением
и смещением 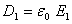 , на второй половине зазора (с диэлектриком)
, на второй половине зазора (с диэлектриком)
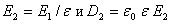 . (2.10)
. (2.10)
Так как электрическое смещение 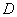 определяется только сторонними зарядами
определяется только сторонними зарядами 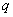 , то
, то
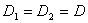 . (2.11)
. (2.11)
Поскольку здесь 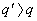 , то
, то 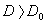 . Определяем соотношения между
. Определяем соотношения между 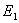 ,
, 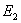 и
и 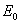
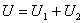
или
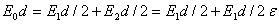 ,
,
откуда
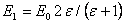 (2.12)
(2.12)
и
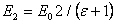 , (2.13)
, (2.13)
т.е. напряженность поля 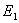 увеличивается по сравнению с
увеличивается по сравнению с 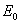 , а его линии начинается на сторонних зарядах
, а его линии начинается на сторонних зарядах 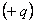 первой обкладки конденсатора и кончаются как на связанных отрицательных зарядах
первой обкладки конденсатора и кончаются как на связанных отрицательных зарядах 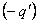 диэлектрика, так и на сторонних зарядах
диэлектрика, так и на сторонних зарядах  на второй обкладке (рисунок 2.2).
на второй обкладке (рисунок 2.2).
Пример 2. Заряд конденсатора остается неизменным (источник после зарядкиотключается, 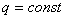 ):
):
а) диэлектрик с проницаемостью 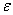 полностью заполняет зазор (рис. 2.1). Под действием поля он поляризуется и на нем появляются связанные заряды
полностью заполняет зазор (рис. 2.1). Под действием поля он поляризуется и на нем появляются связанные заряды 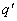 , которые создают поле напряженностью
, которые создают поле напряженностью 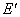 , направленное против поля сторонних зарядов напряженности
, направленное против поля сторонних зарядов напряженности 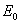 , следовательно, в этом случае напряженность в зазоре равна
, следовательно, в этом случае напряженность в зазоре равна
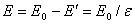 , (2.14)
, (2.14)
т.е. поле ослабляется в 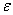 раз.
раз.
Электрическое смещение 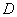 , вследствие постоянства сторонних зарядов, остается неизменным и равным смещению в вакууме
, вследствие постоянства сторонних зарядов, остается неизменным и равным смещению в вакууме
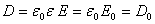 ; (2.15)
; (2.15)
б) диэлектрик заполняет только вторую половину зазора (рис 2.2). В этом случае на воздушной половине зазора, вследствие постоянства сторонних зарядов напряженность поля равна
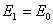 . (2.16)
. (2.16)
Линии 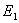 начинаются на сторонних зарядах на первой обкладке
начинаются на сторонних зарядах на первой обкладке 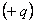 и кончаются как на связанных зарядах
и кончаются как на связанных зарядах 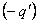 , так и на сторонних зарядах второй обкладки
, так и на сторонних зарядах второй обкладки  .
.
На второй половине зазора с диэлектриком 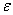 , вследствие его поляризации и появления поля
, вследствие его поляризации и появления поля 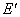 связанных зарядов
связанных зарядов 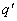 , напряженность равна
, напряженность равна 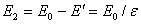 , (2.17)
, (2.17)
т.е. поле в диэлектрике ослаблено в 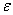 раз. Электрическое смещение так же, как и в первом случае, остается неизменным и равно
раз. Электрическое смещение так же, как и в первом случае, остается неизменным и равно
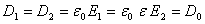 . (2.18)
. (2.18)
 2014-01-27
2014-01-27 753
753








