Экономико-математическая модель оценки альтернатив в условиях неопределенности и риска
Переформулируем постановку задачи (12.1), выполненную ранее, следующим образом.
Пусть имеется несколько конкурирующих инвестиционных проектов решения какой - либо проблемы и «аналитик» должен выбрать наиболее предпочтительный. При каждом отдельном расчете по каждому проекту-конкуренту элементом оценочной матрицы (см. таблицу) является один из четырех показателей (ЧДД, ВНД, срок окупаемости, уровень рентабельности), по которым оценивается ожидаемая эффективность того или иного варианта. Вводится общее для всех показателей эффективности обозначение «u».
Тогда величина u отражает взаимодействие управляемой (выбираемой «аналитиком») альтернативы x´i ÎX´(i=1,...,n) и неуправляемой альтернативы (сценария – состояния внешней среды проекта – «природы») x´´j ÎX´´(j=1,...,m). Все множество элементов uij оценочной матрицы (см. Таблицу 12.1) отражает, таким образом, оценку исходов всех возможных сочетаний пар “альтернатива x´i - сценарий xj´´.
Таблица 12.1
Сценарии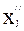 ÎX´´ ÎX´´ | |||||
Альтернативы 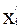 ÎX´ ÎX´ | 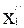 | ... | 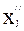 | ... | 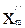 |
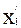 | u11 | ... | u1j | ... | u1m |
| ... | ... | ... | ... | ... | ... |
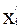 | ui1 | ... | uij | ... | uim |
| ... | ... | ... | ... | ... | ... |
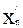 | un1 | ... | unj | ... | unm |
После формирования матрицы //uij// варианты x´iÎX´(i=1,...,n) оцениваются по следующим пяти специальным критериям (правилам).
1. Максиминный критерий Вальда (наибольшей осторожности, обеспечивающий получение гарантированного результата).
Для i-ой строки и j-го столбца матрицы (uij) выбирается u* = 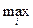
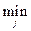 uij
uij
2. Критерий Сэвиджа (минимаксного сожаления).
Используется понятие сожаления для i-й альтернативы при j-ом сценарии Cij= (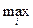 uij) - uij. Далее выбирается u* =
uij) - uij. Далее выбирается u* = 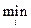
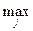 Cij
Cij
3. Критерий максимакса (крайнего оптимизма).
Для i-той строки и j-го столбца матрицы (uij) выбирается u* = 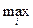
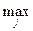 uij.
uij.
4. Критерий Гурвица.
Пусть для i-го варианта mi=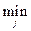 uij, Mi=
uij, Mi=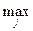 uij. Для каждого варианта вычисляется показатель ui(a) = a×mi+ (1- a)×Mi, где
uij. Для каждого варианта вычисляется показатель ui(a) = a×mi+ (1- a)×Mi, где 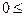 a
a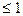 . Далее при заданном a выбирается u*=
. Далее при заданном a выбирается u*=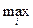 ui(a). В критерии Гурвица параметр a можно интерпретировать как меру осторожности лица принимающего решение. При a = 0 получаем "оптимистический" максимаксный, а при a = 1 - "осторожный" минимаксный критерий.
ui(a). В критерии Гурвица параметр a можно интерпретировать как меру осторожности лица принимающего решение. При a = 0 получаем "оптимистический" максимаксный, а при a = 1 - "осторожный" минимаксный критерий.
5. Критерий Байеса - Лапласа.
Используется, когда известно априорные распределение степеней возможности сценариев P = (p1,…, pm), pi j ≥ 0, 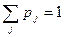 . Для каждой альтернативы вычисляется показатель
. Для каждой альтернативы вычисляется показатель 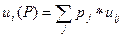 . Далее выбирается u* =
. Далее выбирается u* = 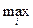 ui(P). Если вероятности (p1,…, pm) равны друг другу, то получаем критерий Лапласа, если нет - критерий Ьайеса.
ui(P). Если вероятности (p1,…, pm) равны друг другу, то получаем критерий Лапласа, если нет - критерий Ьайеса.
Критерии 1-4 применяются для оценки ожидаемой эффективности ИП в условиях радикальной неопределенности, критерии 5 – в условиях риска.
Как оценивается эффективность ИП в условиях неопределенности на практике, покажем на числовых примерах, которые будут проанализированы в следующей лекции. ■
Литература
1. Ларичев О.И. Методы многокритериальной оценки альтернатив // Многокритериальный выбор при решении слабоструктуризованных проблем. Вып. 5. –М.:, 1978, с. 5-30.
2. Кибалов Е.Б. Стратегический менеджмент при строительстве и эксплуатации железнодорожной магистрали в районе хозяйственного освоения: Учебное пособие. – Новосибирск: Сибирская государственная академия путей сообщения, 1997. – 146 с.
3. У. Баумоль. Экономическая теория и исследование операций. Пер. с англ. – М.: «Прогресс», 1965. – 496 с.
Лекция 8. Числовой пример оценки ИП в ситуациях неопределенности и риска
Рассмотрим тот же пример, который анализировался при выдаче индивидуальных заданий для расчетов эффективности ИП в ситуации определенности.
1. Дано:
Проект строительства и эксплуатации мостового перехода N c альтернативными (конкурирующими) технико-технологическими решениями, но с одинаковой пропускной способностью, может быть реализован в трех вариантах, отличающихся уровнем и динамикой затрат (оттоков) средств и результатов (притоков) средств за расчетный период (см. таблицу 1).
 2014-01-28
2014-01-28 1048
1048
