Энергия сигнала

Нормированное линейное пространство.

Для того, чтобы продолжить и углубить геометрическую трактовку теории сигналов, необходимо ввести новое понятие, которое по своему смыслу соответствует длине вектора. Это позволит не только придать точный смысл высказыванию вида “ первый сигнал больше второго”, но и указать, на сколько он больше.

Длину вектора называют его нормой. Линейное пространство сигналов L является нормированным, если каждому вектору S(t)ÎL однозначно сопоставлено число ||S||- норма этого вектора, причем выполняются следующие аксиомы нормированного пространства:

1. Норма неотрицательна, т.е. ||S||³0

||S||=0 тогда и только тогда, когда S=Ǿ

2. Для любого числа a справедливо равенство ||aS||=|a|*||S||

3. Если S(t) и p(t) два вектора и L, то выполняется неравенство треугольника ||S+p|| £ ||S||+||p||

Норма вектора вычисляется по формуле:

||S||=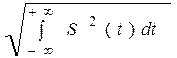

Квадрат нормы носит название энергии сигнала:

Е_s=||S||²=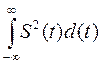

Метрическое пространство: введем еще одно понятие, которое обобщало бы наше обычное представление о расстоянии между точками в пространстве.

Говорят, что линейное пространство становится метрическим пространством, если каждой паре элементов U,V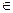L сопоставлено неотрицательное число r(U, V) называемое метрикой или расстоянием между этими элементами. Метрика, независимо от способа ее определения, должна подчиняться аксиомам метрического пространства:

1. r(U, V)=r(V, U)

2. r(U, U)=0 при любых U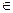L

3. Каков бы ни был элемент W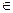L, всегда r(U, V) £ r(U, W)+r(W, V)

Обычно метрику определяют как норму разности двух сигналов r(U, V)=||U-V||.

Норму можно понимать как расстояние между выбранным элементом пространства и нулевым элементом ||U||=r(U, V). Зная метрику, можно судить, насколько хорошо один из сигналов аппроксимирует другой.