Введя понятия нормы и метрики мы все равно лишены возможности вычислить угол между двумя векторами. Это можно сделать, если ввести понятие скалярного произведения сигналов.
Если в обычном трехмерном пространстве известны два вектора 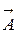 и
и 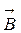 , то
, то
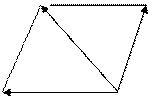
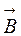
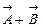
y
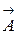
|А+В|2=|А|2+|В|2+2(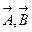 ) (*),
) (*),
где 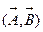 = |
= |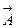 ||
||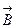 | cosy - скалярное произведение
| cosy - скалярное произведение  этих векторов, зависящее от угла y между ними.
этих векторов, зависящее от угла y между ними.
Действуя по аналогии вычислим энергию суммы 2-х сигналов U и V:
Е=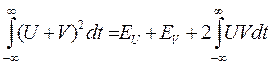 (**)
(**)
В отличии от самих сигналов их энергии неаддитивные- т.е. энергия суммарного сигнала содержит в себе так называемую взаимную энергию 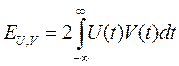
Сравнивая между собой формулы (*) и (**) определим скалярное произведение вещественных сигналов U и V: 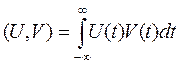 косинус угла между ними
косинус угла между ними 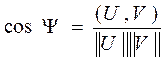 .
.
Скалярное произведение обладает свойствами:
1. (U, U)³0
2. (U, V) = (V, U)
3. (aU, V) = a(U, V), где a- вещественное число
4. (U+V, W) = (U, W)+(V, W)
Линейное пространство с таким скалярным произведением, полное в том смысле, что оно содержит в себе все предельные точки любых сходящихся последовательностей векторов из этого пространства, называется вещественным гильбертовым пространством Н.
Справедливо фундаментальное неравенство Коши-Буняковского 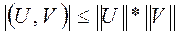 .
.
 2014-01-31
2014-01-31 1001
1001








