Фильтрация случайных сигналов

Рассмотрим задачу оптимальной линейной фильтрации случайных сигналов, когда неизвестна форма полезного сигнала и возникает необходимость восстановления сигнала х(t) или его характеристик. Линейная фильтрация основана на том, что энергетические спектры полезного сигнала и помехи различаются своим частотным содержанием. Предполагается, что полезный сигнал х(t) и помеха x(t) отвечают условиям стационарности, нормально распределены и не коррелированы между собой. Аддитивная смесь z(t) сигнала и помехи, спектральные плотности мощности которых известны, подается на оптимальный линейный фильтр, обеспечивающий фильтрацию с минимальной погрешностью.

Возможны варианты желаемого преобразования полезного сигнала: фильтрация без запаздывания и фильтрация с задержкой или предсказанием. При фильтрации без запаздывания t=0 (т.е. моменты приложения сигнала к входу фильтра и отсчета совпадают). Если t<, то осуществляется фильтрация с задержкой, которую также называют интерполяцией. В этом случае желаемый частотный коэффициент передачи имеет вид

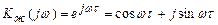. (19)

Однако частотный коэффициент передачи линейного фильтра 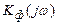имеет несколько иной вид:

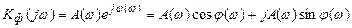, (20)

где 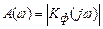- АЧХ фильтра; j(w) – ФЧХ фильтра.

Отличие выражений (19) и (20) является причиной искажения полезного сигнала и появления соответствующей составляющей погрешности фильтрации e_х. Вторая составляющая погрешности фильтрации e_x обусловлена входным шумом, прошедшим через фильтр.

Согласно теории случайных процессов, связь межу дисперсией s стационарного случайного процесса и его спектральной плотностью мощности W(w) может быть представлена в виде

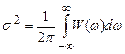, (21)

а связь между спектрами мощности выходного случайного сигнала с аналогичным спектром на входе системы – в виде

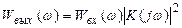. (22)

Используя (21) и (22), получим выражение для дисперсии суммарной погрешности фильтрации

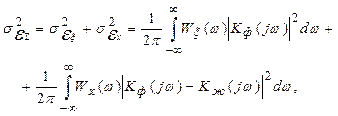
(23)

или, после преобразования,

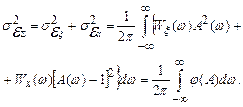
(24)

Минимум подынтегральной функции найдем из условия

.

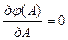После дифференцирования получим выражения АЧХ оптимального фильтра и дисперсии его суммарной погрешности:

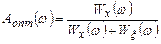; (25)

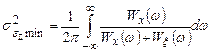. (26)

Для определения АЧХ подставим в (23) тригонометрические представления K_ф(jw) и K_ж(jw) из формул (19) и (20). Получим после преобразования:

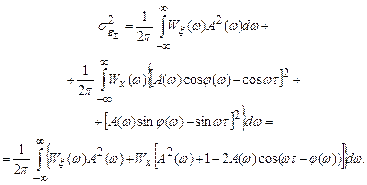
(27)

Условием минимума 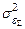является наибольшее значение 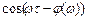или

,

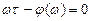тогда оптимальная фазочастотная характеристика фильтра определяется выражением

.

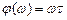Для решения задач фильтрации случайных сигналов, наряду с методами оптимальной линейный фильтрации с интерполяцией находит применение метод экстраполяции (прогнозирования). Задача оптимальной экстраполяции сводится к поиску такого линейного алгоритма обработки входного сигнала z(t), который позволял бы получить оценку 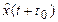того значения полезного сигнала 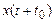, которое он примет на момент времени t+t_э, где t – момент наблюдения сигнала на выходе фильтра, t_э – время экстраполирования.

Предполагается, что фильтр должен представлять собой инерционную линейную систему, сигнал 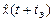на выходе которой должен зависеть не только от смеси z(t) полезного сигнала с аддитивной помехой в момент времени t, но и от его значений в предыдущие моменты времени. Величина сигнала формируется на выходе линейной системы путем сложения (суперпозиции) всех значений z(t), каждое из которых умножено на импульсную переходную функцию h(t,t) (t - момент приложения сигнала к входу фильтра).

В общем случае связь процесса 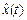на выходе линейной системы с процессом на входе сигнала z(t) описывается выражением

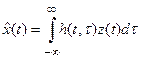. (28)

Следовательно, свойства фильтра полностью определяются функцией h(t,t).

Условием физической осуществимости фильтра является h(t,t)=0 при t<t, т.е. сигнал на выходе 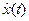в данный момент времени зависит только от значений, предшествующих этому моменту z(t). Поэтому верхний предел интегрирования в выражении (28) следует ограничить значением t. Если z(t)=0 при t<0, то нижний предел интегрирования равен нулю. Учитывая стационарность входного сигнала, можно допустить, что линейный фильтр имеет постоянные параметры, а его h(t,t) зависит только от разности t-t, т.е. h(t₁–t)= h(t–t). Учитывая сказанное, выражение (28) преобразуем к виду

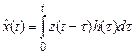. (29)

Для фильтра с предсказанием

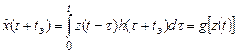. (30)

Погрешность фильтрации с экстраполяцией является случайным процессом с математическим ожиданием, равным нулю. Оценка отвечает требованию несмещенности. Поэтому, как и в задаче оптимальной фильтрации, близость оценки 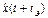к истинному значению х(t+t_э) определяется дисперсией 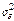погрешности экстраполяции e:

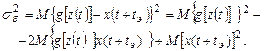(31)

Подставив в (31) значение g[z(t)] из выражения (30) и заменив произведение двух одинаковых интегралов {g[z(t)]}² двойным интегрированием с переменными t и t`, получим:

;

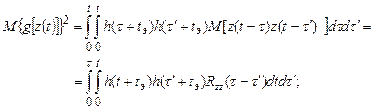
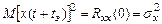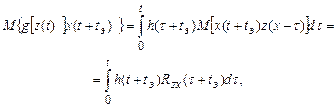
где 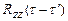– корреляционная функция входного сигнала z(t); R_zx(t+t_э) – взаимная корреляционная функция полезного х(t) и входного z(t) сигналов.

Следовательно, дисперсия погрешности фильтрации с экстраполяцией определяется выражением

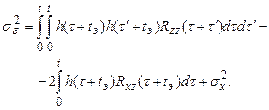(32)

Для того чтобы определить оптимальную импульсную характеристику фильтра-экстраполятора, следует найти минимум 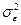. Задача может быть решена двумя способами: либо решением интегрального уравнения Винера-Хопфа, либо путем решения дифференциальных уравнений с заданными начальными условиями (метод фильтрации Калмана-Бьюси). Техническая реализация фильтров как одного, так и другого связана со значительными трудностями, поэтому в аналоговой линейной фильтрации используются в основном фильтры Баттерворта и им подобные.