Марковские процессы с непрерывным временем и дискретным состоянием. Пуассоновские потоки событий

При исследовании различных систем требуется анализироватьпроцессы блуждания системы по состояниям подмножества YX и в связи с этим составлять ориентированные графы для этих подмножеств состояний Y.

Такие процессы называют дискретными случайными процессами. Число состояний процесса может быть как конечным, так и бесконечным (счетным). В основном будем рассматривать системы с конечным числом состояний, что вполне достаточно при рассмотрении принятых задач.

Классификация групп состояний.

Классификация состояний. Ориентированный граф состояний.

ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ ПРИКЛАДНОЙ ТЕОРИИ МАРКОВСКИХ СЛУЧАЙНЫХ ПРОЦЕССОВ С НЕПРЕРЫВНЫМ ВРЕМЕНЕМ И ДИСКРЕТНЫМИ СОСТОЯНИЯМИ

Рассмотрим системы (процессы) Х (t) которые в любой момент времени t могут находиться в одном из своих состояний xo,x1..,xn.

Событие, состоящее в том, что система в момент времени t находится в состоянии x į, обозначим

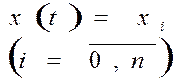
а вероятность этого события

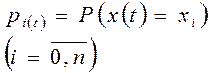
Очевидно, что для любого момента времени t должно выполняться условие

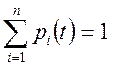
Одна из основных задач исследования обычно состоит в отыскании вероятностей p ί (t) для различных систем и процессов.

Обозначим через x множество всех состояний: 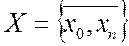В процессе функционирования какой-либо системы процесс может переходить из одного состояния в другое.

Например, если в начальный момент t =0 процесс находился в состоянии 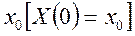, то в какой-то момент времени t0 он может перейти в состояние 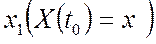. Будем считать, что переход процесса из одного состояния в другое осуществляется мгновенно (скачком), т. е. время перехода из состояния в состояние равно нулю.

Т.о. рассматриваемую систему (процесс) можно интерпретировать как некоторую точку, которая в какие-то моменты времени (в общем случае случайные) перескакивает из одного состояния в другое, определяя динамический характер самой системы. То есть точка осуществляет случайные блуждания по своим возможным состояниям. Множество всех состояний системы (процесса) можно рассматривать как множество вершин некоторого графа, а процесс перехода из состояния в состояние – как процесс блуждания точки по вершинам этого графа.

Вершину графа 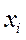(состояние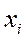) будем изображать в виде прямоугольника с вписанным внутри него обозначением состояния.

	X ί

Вершина графа 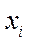может быть либо соединена, либо не соединена с вершиной (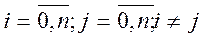). Это эквивалентно тому, что система (процесс), попав в состояние 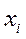либо может непосредственно перейти из этого состояния в состояние 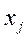(минуя все другие состояния), либо такого непосредственного перехода осуществить не может (хотя в этом случае вообще возможен переход из состояния 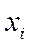в состояние через другие состояния).

Линии, соединяющие вершины, назовем ребрами. Т. о., каждой паре вершин и можно поставить в соответствие некоторое число (ребро) 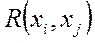, которое может принять два значения:

1) 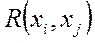=1, если вершина соединена ребром с вершиной (т. е. если возможен непосредственный переход из состояния в);

2) 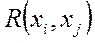= 0, если вершина не соединена ребром с вершиной (т. е. если возможен непосредственный переход из состояния в ).

Cсхематически возможность непосредственного перехода из состоянияв состояние изображается следующим образом:

Между вершиной и проводится ориентированное ребро, которое представляет собой стрелку, выходящую из вершиныи входящую в вершину

Если непосредственный переход из в – не возможен, то на схеме ребра не будет.

Для ориентированного ребра 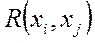вершинаназывается начальной вершиной– процесс перехода из состояния в состояние, то 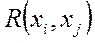=0 для любых 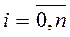(петли в графах состояний не рассматриваются).

Если 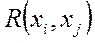=1,то будем говорить, что вершина является соседней по отношению

Если 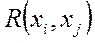= = 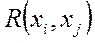1, то вершины также соседние.

Т.о. любой дискретный процесс характеризуется ориентированным графом состояний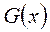, который представляет схему возможных переходов из состояния в состояние. Такому ориентированному графу состояний соответствует квадратная матрица размерности 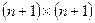, состоящая из нулей и единиц, элементами которой 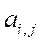являются ребра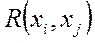

║║ = ║║

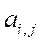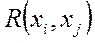По главной диагонали этой матрицы стоят нули, т. к

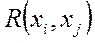= 0 ()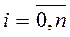

Дадим следующую классификацию состояний:

Состояниеназывается изолированным, если выполняется условие:

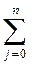
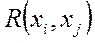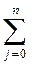
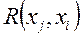== 0,

т. е. если система не может перейти в состояниеили выйти из него.

Состояние называется концевым (поглощающим), если выполняются совместно два условия:

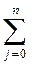
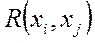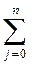
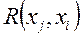= 0; >0

т. е. если из состояния система уже ни в какое другое состояние перейти не может, но хотя бы из одного состояния (ί≠j) может перейти в состояние состояние называется начальным (источником) если выполняются совместно два условия:

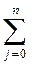
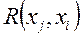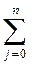
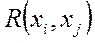= 0, >0

Эти условия эквивалентны тому, что система может выйти из состояния (если он в нем находилась) и перейти в какое-либо другое состояние, но попасть в из какой-либо другого состояния она не может

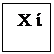Состояние называется транзитивным, если выполняются два неравенства

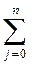
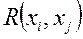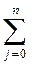
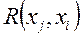> 0, > 0.

Система, попав в транзитивное состояние, рано или поздно его покинет.

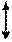Маршрутом при блуждании точки по вершинам (состояниям),
образующим множество Х, называется такая последовательность ребер, когда два соседних ребра имеют общую (промежуточную) вершину.

Например: M []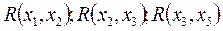

Это маршрут, выходящий из вершины 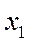, проходящий через вершины 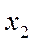и 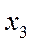и заканчивающийся в вершине .

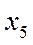Маршрут, связывающий вершины 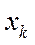, 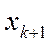…,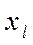будем обозначать M (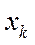…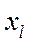). Вершину 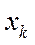будем называть началом маршрута, вершину xℓ -концом маршрута, все остальные вершины –промежуточные.

Положим M (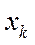…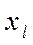)=1,если маршрут проходящий через вершины 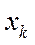…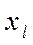существует и M (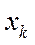…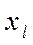) =0, если такого маршрута не существует. Очевидно что в этом случае

M (…) =,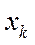

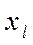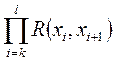так как для существования маршрута между вершинами 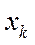…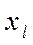нужно существование ребер между этими вершинами.

Если 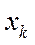=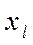то маршрут называется циклическим.

Маршрут между вершинами 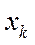…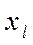называется путем, а циклический маршрут –контуром [П (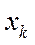…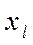) ], если каждое ребро, из которого состоит маршрут, встречается в нем один раз. Если путь между вершинами 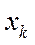…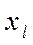существует, то будем считать П (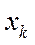…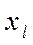)=1,в противном случае П(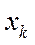…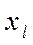)=0

Если маршрут М (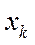…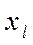)=1, то и путь П (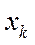…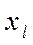) =1. Из нескольких путей, связывающую вершины 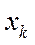и 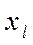будем считать минимальным тот путь, который состоит из минимального числа ребер. Такой путь может быть не единственным.

Состояние (вершина) называется связанным с состоянием путем, состоящим из одного ребра:

M () = П (,)=R , )=1

Состояния (вершины) и называются взаимно –связанными, если маршруты М (,)=M (, )=1

Состояния , и называются связанными, если выполняется одно из условий:

а) М(, …)=1 и М (…) =0

в) М (, …)=0 и М (, …)=1

Перейдем классификации групп состояний (подмножеств состояний).

Рассмотрим некоторые подмножества состояний Y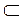X, при этом не будем рассматривать случай, когда подмножество Y является пустым.

Подмножество состояний Y называется замкнутым (концевым) если не существует маршрута, соединяющего любое состояние этого множества с каким-либо состоянием множества 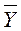, являющееся дополнением множестваY:

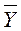M (…) =0 (Î Y; ХÎ=X-Y)

Подмножество Y называется связным, если любые два состояния Î Y и Î Y являются связными.

Подмножество Y эргодическим, если оно является замкнутым и связным одновременно.

Подмножество состояний Y незамкнутым если для любого состояния Î Y- существует маршрут, выводящий процесс за пределы подмножества Y, т. е. найдется такое Î Y, что М (…)= 1 (Î Y)

Подмножество состояний Y называется начальным, если для любого

Î Y не существует маршрута, соединяющего состояния с каким –либо состоянием Î Y:

М (…)=0 (Î Y, Î )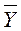

И с другой стороны подмножество Y является незамкнутым. Если в какой- либо момент времени t известно, что система не находится в начальном подмножестве состояний, то она никогда не вернется туда не вернется.

Подмножество состояний Y называется транзитивным, если оно является не замкнутыми и для любого состояния Î Y найдется хотя одно такое состояние Î Y, что М (… )= 1.

Ориентированным подграфом G (Y) состояний подмножеств Y называется такая часть ориентированного графа G (Y), множество вершин которого равно Y, а ребро 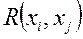этого под графа G (Y) равно ребру G (X), если Î Y, Î Y.

Другими слвами, ребро 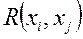подграфа G (Y) остается таким же, как и ребро графа G (X), если начальная и конечная вершина этого ребра принадлежит множеству Y.

Преобразованным ориентированным подграфом G (Y) состояний подмножества Y называется такая часть ориентированного графа G (X), множество вершин которого равна Y, а хотя бы одно ребро 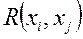этого подграфа G (Y) не равно ребру графа G (X), если Î Y и Î Y, т. е. часть ребер преобразуется (либо исключается, либо вводятся новые).

Обозначим 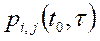условную вероятность того, что в момент времени 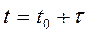система будет в состоянии , если в момент 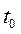она была в состоянии .

Дискретный случайный процесс называется марковским, если вероятность 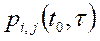зависит только от указанных в обозначении вероятности параметров: в таком состоянии . была система в момент 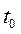и в какое состояние система должна попасть в момент.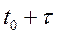

Другими словами, все вероятностные характеристики марковского случайного процесса в будущем (t > to) зависит лишь от того, в каком состоянии система находится в настоящий момент времени to и не зависит от того, каким образом этот процесс протекал в прошлом до момента to.

Различают 2 типа марковских процессов: с дискретным временем и с непрерывным временем.

Марковским случайным процессом с дискретным временем называется процесс, у которого переходы из одного состояния в другое возможны в строго определенные, заранее известные, неслучайные моменты времени 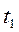,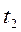…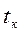. Такие процессы очень редко встречаются при решении различных прикладных задач, поэтому они не анализируются.

Марковским случайным процессом с непрерывным временем называется процесс, у которого переход из одного состояния в другое (соседнее) состояние возможен в любой момент времени t.

Марковские случайные процессы с непрерывным временем тесно связаны с пуассоновскими потоками. Можно доказать, что если все потоки событий, переводящие систему из состояния в состояние, являются пуассоновскими, то случайный процесс, протекающий в системе будет марковским с непрерывным временем.

Докажем это утверждение. Рассмотрим систему, состоящую из двух состояни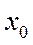й: и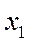– которая может переходить только из состояния в состояние 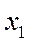под воздействием пуассоновского потока событий с интенсивностью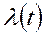

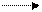
Это ориентир граф. Состояния такой системы.

X1

xо

Обозначим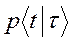–условную вероятность того, что система в момент

Времени t находится в состоянии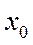, вычисляемую при условии, что в момент t < t (t ³ 0) она находилась в этом же состоянии. Если процесс протекающий в такой же системе, марковский, то по определению имеет следующее равенство справедливое для любых s>0 и t> 0:

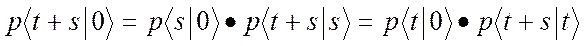
Покажем, что это равенство имеет место, если поток, переводящий систему из состояния 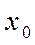в состояние 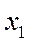, является Пуассоновским.

Для вероятности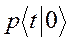можно составить следующее дифференциальное уравнение:

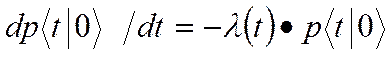(1)

решение этого дифференциального уравнения имеет вид

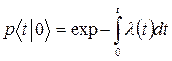
обозначим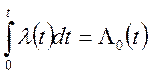

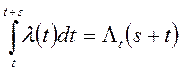
c учетом принятых обозначений:

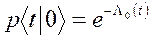
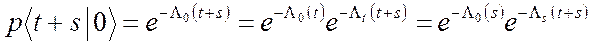
Решая уравнение (1) можно убедиться, что

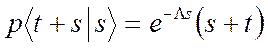
В результате получаем, что

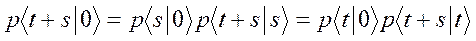
т. е. наш процесс является марковским с непрерывным временем.

Для сведения произвольного процесса к марковскому с непрерывным временем достаточно принять в нем все потоки событий пуанссоновскими, которые определяются своими интенсивностями. Т. е. необходимо, определить интенсивности всех потоков событий, переводящие систему из состояния в состояние и считать, что на систему воздействуют пуанссоновские потоки событий с известными интенсивностями.

Лекция №20