Ранее мы рассмотрим приближенные методы построения доверительных интервалов для оценок.
Для точного нахождения доверительных интервалов совершенно необходимо знать заранее вид закона распределения величины 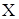 , тогда как для применения приближенных методов это не обязательно.
, тогда как для применения приближенных методов это не обязательно.
Доказано, что при нормальном распределении величины 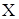 случайная величина:
случайная величина:
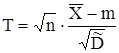
подчиняется так называемому закону распределения Стьюдента с 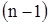 степенями свободы. Плотность этого закона имеет вид:
степенями свободы. Плотность этого закона имеет вид:
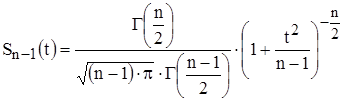 .
.
Он не зависит от неизвестных параметров 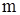 и
и 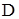 , а зависит только от
, а зависит только от 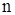 .
.
Пусть произведено 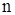 независимых опытов над случайной величиной
независимых опытов над случайной величиной 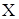 , распределенной по нормальному закону с неизвестными параметрами
, распределенной по нормальному закону с неизвестными параметрами 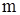 и
и 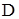 . Для этих параметров получены оценки:
. Для этих параметров получены оценки:
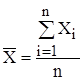 ;
;
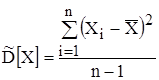 .
.
Требуется построить доверительный интервал для математического ожидания, соответствующий доверительной вероятности 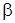 .
.
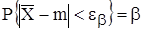 , или
, или
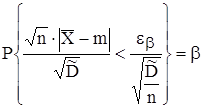 , или
, или
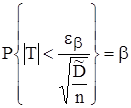 ,
,
где 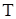 - случайная величина, распределенная по закону Стьюдента.
- случайная величина, распределенная по закону Стьюдента.
Так как
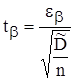 , то
, то
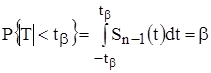 ,
,
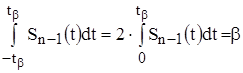 .
.
Величину 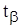 - находят из таблиц распределения Стьюдента.
- находят из таблиц распределения Стьюдента.
Отсюда
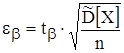 .
.
Доверительный интервал:
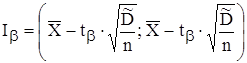 .
.
 2014-01-31
2014-01-31 708
708








