Изучение эконометрических моделей спроса начнем непосредственно с примерами, выводами и рекомендациями. Безусловно, в основу их построения положены выше приведенные математические аппараты, измеряющие модели.
Но все же для ясности немного о спросе как многофакторной системе.
Спрос – это желание и способность покупать товары. На спрос влияют множество внутренних и внешних факторов, в частности цена, насыщенность рынка, качество товара, покупательная способность, уровень конкуренции и т.д., т.е. функцию спроса в общем виде можно представить следующим образом:
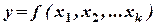 ,
,
где у – спрос;
х1, х2, … хк – факторы, которые оказывают непосредственное влияние на спрос.
В зависимости от конкретных обстоятельств функция спроса может иметь прямопропорциональный, обратнопропорциональный характер, а иногда смешанный характер.
В большинстве случаев кривая спроса опускается вниз (рис. 19). Действительно, кривая спроса описывает взаимоотношение между количеством товара, которое люди желают купить и могут купить в зависимости от цены товара. Низкая цена позволит покупателям купить большее количество товара, который ранее не могли позволить себе купить.
|
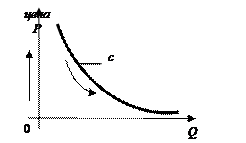
Рис. 19. Кривая зависимости спроса от цены товара
В отличие от спроса, предложение – это желание и способность производителей производить и представлять товары для продажи на рынке.
Кривая предложения (рис. 20) описывает взаимоотношения между ценой товара и количеством этого же товара, которое производители хотят предложить на рынке.
|
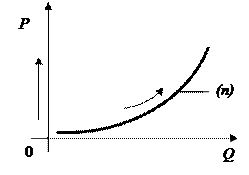
Рис. 20. Кривая зависимости предложения от цены товара
Кривая поднимается вверх, потому что чем выше цена товара, тем большее число фирм имеет возможность производить и продавать товар. Например, более высокая цена дает возможность соответствующим фирмам расширить объем производства за короткий промежуток времени за счет привлечения дополнительных резервов.
Спрос и предложение взаимосвязаны. Наибольший интерес представляет состояние равновесия, т.е. состояние, при котором спрос и предложение характеризуются равенством.

Рис. 21. Кривые спроса и предложения
При равновесном состоянии кривые спроса и предложения пересекаются (рис. 21). В точке пересечения нет ни дефицита, ни избыточного предложения, а значит, нет давления на изменение цены в дальнейшем.
Практически задача сводится к тому, что если цены на товары увеличились, напои мер на 15,3%, как при этом изменится спрос?
Пример 1. Предположим, имеются данные, характеризующие динамику спроса в зависимости от цены
у - спрос х - цена
35,4 18,1
36,2 17,4
36,8 17,1
37,1 16,8
37,7 16,3
37,9 16,1
Требуется исследовать, измерить дальнейшее поведение спроса, если тенденция снижения цен сохранится.
Решение аналогичных задач в основном состоит из четырех последовательных и в то же время взаимосвязанных этапов: анализ исходной информации, следовательно, определение тенденции поведения системы; выбор математической формы связи; решение системы; анализ результатов решения системы, следовательно, обоснование конкретных выводов и рекомендации.
Этап 1. Анализ данных. Анализ данных дает основание утверждать, что спрос увеличивается, а цена снижается. Уровень роста спроса составляет около 7,1%, а уровень снижения цен - 11,0%.
Итак, со снижением цен, спрос увеличивается, причем уровень снижения цен выше, чем уровень увеличения спроса.
Этап 2. Выбор функции связи. Есть основание утверждать, данная зависимость имеет обратнопропорциональный характер, типа y = a + 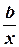 ,
,
где у - спрос;
х - цена;
a и b - параметры системы;
Этап 3. Решение системы. Составляем систему стандартных уравнений:
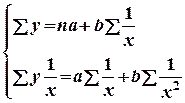 (1)
(1)
Для решения системы (1) желательно составлять вспомогательную рабочую таблицу.
Для решения параметров а и b
| № пп | у | х | 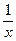
| у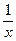
| х2 | 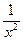
| х · у | у2 |
| 35,4 | 18,1 | 0,055 | 1,96 | 327,61 | 0,003 | 640,74 | 1253,16 | |
| 36,2 | 17,4 | 0,057 | 2,08 | 302,76 | 0,003 | 629,88 | 1310,44 | |
| 36,8 | 17,1 | 0,058 | 2,15 | 292,41 | 0,003 | 629,28 | 1354,24 | |
| 37,1 | 16,8 | 0,060 | 2,21 | 282,24 | 0,004 | 623,28 | 1376,41 | |
| 37,7 | 16,3 | 0,061 | 2,31 | 265,69 | 0,004 | 614,51 | 1421,29 | |
| 37,9 | 16,1 | 0,062 | 2,35 | 259,21 | 0,004 | 610,19 | 1436,41 | |
| ∑ | 221,1 | 101,8 | 0,353 | 13,06 | 1729,9 | 0,021 | 3747,9 | 8151,95 |
На основе данных таблицы составляем систему стандартных уравнений в количественном отношении:
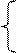 221,1 = 6 а + 0,353 b
221,1 = 6 а + 0,353 b
13,06 = 0,353 а + 0,021 b, (2)
Путем решения системы (2) имеем:
у = 18,61 + 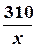 .
.
Чтобы предвидеть возможные изменения спроса, вычисляем количественные характеристики спроса на основе полученной функции.
Итак,
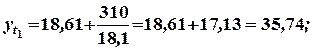
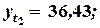
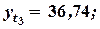
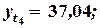
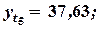
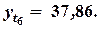
Таким образом, спрос увеличивается. Уровень роста составляет 6,0%, т.е. по выявленной функции уровень роста на 1,0% ниже по сравнению с заданной функцией спроса.
В данном случае коэффициент корреляции r = 0,84; Дr = 70,6%.
Вывод. Увеличение спроса с 36,43 до 37,86 единиц, т.е. на 6,0% является адекватным на уровне 70,6%. На 29,4% вывод относительно снижения спроса следовало бы доисследовать за счет других факторов.
Пример 2. Предположим, имеются данные, характеризующие последовательность изменения спроса (у) в зависимости от двух факторов: х (цена), z (насыщенность потребительского рынка).
у (спрос) {29,4; 29,9; 30,1; 30,4; 30,9; 31,4};
х (цена) {28,3; 31,2; 33,5; 36,4; 37,5; 38,8};
z (насыщ. рынка) {84,5; 85,6; 86,9; 87,8; 89,5; 90,8}.
Данные дают основания утверждать, что спрос возрастает, уровень роста составляет 6,8%. Возрастают цены, а также насыщенность потребительского рынка, хотя насыщенность рынка не превышает 100%.
Требуется оценить поведение спроса в дальнейшем, если тенденция сохранится.
Есть основания полагать, что данная зависимость носит прямопропорциональный характер следующего вида:
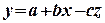 .
.
Составляем систему стандартных уравнений:
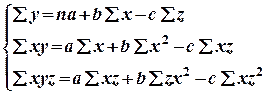
Для решения системы также составляем рабочую таблицу.
Затем составляем систему стандартных уравнений в количественном отношении:
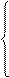
| 182,1 = 6 a + 205,7 b – 525,1 z | : 6 |
| 6256,88 = 205,7 a + 7133,23 b – 18048,43 c | : 205,7 | |
| 549273,38 =18048,43 a +627410,01 b –1584539,83 c | :18048,43 |
Для расчета параметров системы стандартных уравнений
| № пп | у | х | z | x2 | z2 | xy | xz | xyz | zx2 | xz2 | y2 | z2y |
| 29,4 | 28,3 | 84,5 | 800,89 | 7140,25 | 832,02 | 2391,35 | 70305,69 | 67675,265 | 202069,08 | 864,36 | 2484,3 | |
| 29,9 | 31,2 | 85,6 | 973,77 | 7327,36 | 932,88 | 2670,72 | 79854,528 | 23326,464 | 228613,63 | 894,01 | 2559,44 | |
| 30,1 | 33,5 | 86,9 | 1122,25 | 7551,61 | 1008,35 | 2911,15 | 87625,615 | 97523,525 | 252978,94 | 906,01 | 2615,69 | |
| 20,4 | 36,4 | 87,8 | 1324,96 | 7708,84 | 1106,56 | 3195,92 | 97155,968 | 116331,49 | 280601,78 | 924,16 | 2669,12 | |
| 30,9 | 37,5 | 89,5 | 1406,25 | 8010,25 | 1158,75 | 3356,25 | 103708,13 | 125859,38 | 300384,38 | 954,81 | 2765,55 | |
| 31,4 | 38,8 | 90,8 | 1505,44 | 8244,64 | 1218,32 | 3523,04 | 110623,46 | 136693,95 | 319892,03 | 985,96 | 2851,12 | |
| Сумма | 182,1 | 205,7 | 525,1 | 7133,23 | 45982,95 | 6256,88 | 18048,43 | 549273,38 | 627410,01 | 1584539,83 | 5529,31 | 15945,22 |
Получим:
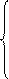 30,35 = а + 34,2833 b – 87,5166 c (1)
30,35 = а + 34,2833 b – 87,5166 c (1)
30,4175 = a + 34,6778 b – 27,7415 c (2)
30,4333 = a + 34,7625 b – 87,79993 c (3)
(2) – (1)
(2) – (3)
Имеем:
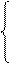
| 0,10675 = 0,3945 b – 0,2249 c | : 0,3945 |
| -0,0158 = -0,0847 b + 0578 c | : -0,0847 |
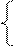 0,1711 = b – 0,5701 c
0,1711 = b – 0,5701 c
0,1865 = b – 0,6729 c
В итоге, с = -0,18; b = 0,16; а = 29,3.
Имеем, у = 29,3 + 0,16 + 0,18 z.
Итак, уt(1) = 29,3 + 0,16 + 0,18 = 29,64;
уt(2) = 29,3 + 0,16 ∙ 2 + 0,18∙ 2 = 29,98;
уt(3) = 30,32; уt(4) = 30,66
уt(5) = 31,0; уt(6) = 31,34.
Таким образом, на основе выявленной функции спрос увеличивается с 29,64 до 31,34, т.е. на 5,7%. В данном случае коэффициент множественной корреляции Ry(x,z) = 0,91; DR = 82,8%.
Вывод. Учитывая неполную насыщенность потребительского рынка с ростом цен, будет иметь место увеличение выпуска продукции на 5,7%. Данный вывод является адекватным на уровне 82,8%.
Рассмотрим еще пример. Имеются данные:
у (спрос) {18,3; 19,4; 20,9; 21,4; 22,3};
х1 (цена) {22,9; 23,4; 24,8; 25,8; 26,4};
х2 (н.р.) {122,9; 123,4; 125,9; 126,8; 127,7}.
Требуется дальнейшее поведение спроса.
Решение. Выбираем функцию:
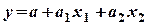 .
.
Составляем систему стандартных уравнений:
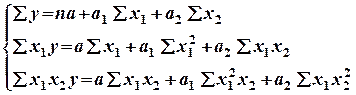
Составляем рабочую таблицу:
После решения получим функцию спроса:
у = -75,5352 + 0,0007347 х1 + 0,7737 х2
уt1 = 18,57; уt2 = 19,56;
уt3 = 21,89; уt4 = 22,59;
уt5 = 23,29.
Спрос увеличивается на 6,0%.
Расчет коэффициента множественной корреляции:
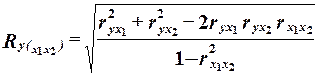 .
.
| у (спрос) | х2 (емкость) | х1 (цена) | ух1 | х12 | х1х2 | ух1х2 | х2х12 | х1х22 | |
| 18,3 | 122,9 | 22,9 | 419,07 | 524,41 | 2814,41 | 51503,7 | 64449,99 | ||
| 19,4 | 123,4 | 23,4 | 453,96 | 547,56 | 2887,56 | 56018,66 | 67568,9 | 356324,9 | |
| 20,9 | 125,9 | 24,8 | 518,32 | 615,04 | 3122,32 | 65256,49 | 77433,54 | 393100,1 | |
| 21,4 | 126,8 | 25,7 | 549,98 | 660,49 | 3258,76 | 69737,46 | 83750,13 | 413210,8 | |
| 22,3 | 127,7 | 26,4 | 588,72 | 696,96 | 3371,28 | 75179,54 | 89001,79 | 430512,5 | |
| ∑ | 102,3 | 626,7 | 123,2 | 2530,05 | 3044,46 | 15454,33 | 317695,9 | 382204,4 |
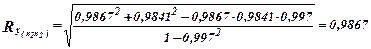
DR = R2 ∙ 100 = 97,3%.
Вывод. Полученные данные позволяют спрогнозировать дальнейшее развитие ситуации на рынке. С достоверностью 97,3% можно утверждать, что при дальнейшем увеличении цены на продукцию спрос будет расти.
Пример 4. Обратно пропорциональная функция спроса в условиях перенасыщенности рынка.
Предположим, имеются данные:
у (спрос) {39,3; 38,8; 38,1; 37,8; 37,1; 36,8};
х (цена) {8,7; 8,84; 8,86; 8,96; 9,01; 9,17};
z (н.р.) {135,8; 141,4; 135,9; 145,5; 139,8; 147,3}.
Нужно предвидеть изменение спроса при сохранении тенденции.
Решение. Анализ данных дает основание утверждать, что спрос снижается, уровень снижения спроса составляет 6,4%; при этом цены на товары возрастают на 5,4%; уровень насыщенности также возрастает.
В данном случае в качестве функции спроса можно выбрать функцию следующего вида:
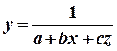 ,
,
где х - цена;
х – насыщенность рынка;
у - спрос;
a, b, с - параметры системы.
Система стандартных уравнений в данном случае имеет вид:
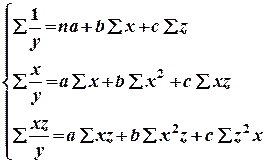
Составляем рабочую таблицу.
Имеем систему уравнений:
 0,158048 = 6 а – 53,54 b + 845,7 с
0,158048 = 6 а – 53,54 b + 845,7 с
1,410834 = 53,54 а - 477,8858 b + 7549,529 с
199,0267 = 7549,529 а – 67412,83 b + 1065564 с
 0,0263413 = а – 8,9233 b + 140,95 c
0,0263413 = а – 8,9233 b + 140,95 c
0,0263510 = a – 8,9258 b + 141,0073 c
0,0263628 = a – 8,9294 b + 141,1431 c
 0,0000097 = -0,0025 b + 0,0573 c
0,0000097 = -0,0025 b + 0,0573 c
- 0,0000118 = 0,0036 b – 0,1358 c
 0,00388 = - b + 22,92 c
0,00388 = - b + 22,92 c
0,00328 = b + 37,72 c
0,00716 = 60,64 c
c = 0,000118073
b = 0,001173766
a = 0,0104738661478 – 0,01664238935 +
+ 0,0263413 = 0,0201073.
| № пп | у | z | х | z 2 | у 2 | x 2 | xz | 1 у | х у | хz y | x2z | z2x |
| 39,3 | 135,8 | 8,7 | 18441,64 | 1544,49 | 75,69 | 1181,46 | 0,025445 | 0,221374 | 30,0626 | 10278,7 | 160442,3 | |
| 38,8 | 141,4 | 8,84 | 19993,96 | 1505,44 | 78.1456 | 1249,976 | 0,025773 | 0,227835 | 32,21588 | 11049,79 | 176746,6 | |
| 38,1 | 135,9 | 8,86 | 18468,81 | 1451,61 | 78,4996 | 1204,074 | 0,026247 | 0,232546 | 31,60299 | 10668,1 | 163633,7 | |
| 37,8 | 145,5 | 8,96 | 21170,25 | 1428,84 | 80,2816 | 1303,68 | 0,026455 | 0,237037 | 34,48889 | 11680,97 | 189685,4 | |
| 37,1 | 139,8 | 9,01 | 19544,04 | 1376,41 | 81,1801 | 1259,598 | 0,026954 | 0,242857 | 33,95143 | 11348,98 | 176091,8 | |
| 36,8 | 147,3 | 9,17 | 21697,29 | 1354,24 | 84,0889 | 1350,741 | 0,027174 | 0,249185 | 36,70492 | 12386,29 | 198964,1 | |
| Сумма | 227,9 | 845,7 | 53,54 | 8661,03 | 477,8858 | 7549,529 | 0,158048 | 1,410834 | 199,0267 | 67412,83 |
Функция спроса имеет вид:
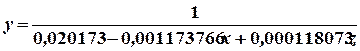 .
.
Найдем варианты спроса на основе полученной функции:
у(х, z)(1) = 38,47; у(х, z)(2) = 37,75;
у(х, z)(3) = 38,73; у(х, z)(4) = 37,26;
у(х, z)(5) = 38,31; у(х, z)(6) = 37,31.
В целом спрос снижается. В данном случае DR = 96%.
Вывод. При постоянно увеличивающейся насыщенности рынка и роста цен нужно хотя бы стабилизировать цены. В противном случае фирме следует переориентироваться на другой вид деятельности.
2.4. Эконометрические модели ценообразования
Пример. Имеются данные:
z (спрос) {31,7; 32,8; 33,8; 34,8; 36,4};
х (н.р.) {90,6; 91,8; 92,4; 92,9; 93,1};
y (цена.) {90,4; 92,4; 93,8; 94,1; 94,7}.
Требуется определить по каким ценам возможно выставлять товар на рынке.
Итак, имеем.
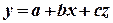 ,
,
где у - цена;
х – насыщенность рынка;
z - спрос;
a, b, с - параметры системы.
Составляем систему:
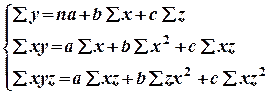
Составляем рабочую таблицу.
Решаем систему:
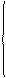 465,4 = 5 а + 460,4 b + 169,5 с
465,4 = 5 а + 460,4 b + 169,5 с
42898,14 = 460,8 а + 42471,38 b + 15627,94 с
1455940 = 15627,94 а + 1441034 b + 531226 с
а = -71,3338
b = 1,80495
c = -0,05794
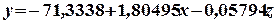
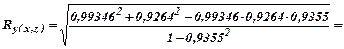 0,9935.
0,9935.
D = r2 ∙ 100% = 0,99352 ∙ 100% = 98,7%.
Вывод. Полученные данные позволяют спрогнозировать дальнейшее развитие структуры на рынке. С достоверностью 98,7% можно утверждать, что при данной цене прибыль будет максимальной.
Как известно цена – это соотношение, при котором товары и услуги обмениваются на деньги. На самом деле, через механизмы ценообразования происходит "перелив" ресурсов из одного сектора экономики в другой и внутри отдельных секторов. Этот "перелив", как правило, осуществляется, в основном, под воздействием товарно-денежных отношений.
| z (спрос) | х (насыщ.) | у (цена) | ху | xzy | x2 | xz | xz2 | zх2 |
| 31,7 | 90,6 | 90,4 | 8190,24 | 259630,6 | 8208,36 | 2872,02 | 91043,03 | |
| 32,8 | 91,8 | 92,4 | 8482,32 | 278220,1 | 8427,24 | 3011,04 | 98762,11 | 276413,5 |
| 33,8, | 92,4 | 93,8 | 8667,12 | 292948,7 | 8537,76 | 3123,12 | 105561,5 | 288576,3 |
| 34,8 | 92,9 | 94,1 | 8741,89 | 304217,8 | 8630,4 | 3232,92 | 112505,6 | 300338,3 |
| 36,4 | 93,1 | 94,7 | 8816,57 | 320923,1 | 8667,61 | 3388,84 | 123353,8 | |
| 169,5 | 460,8 | 465,4 | 42898,14 | 42471,38 | 15627,94 |
Как известно, мощным двигателем экономики является конкуренция. Именно она двигает экономику вперед, используя такой действенный механизм как механизм ценообразования.
Экономика находится под воздействием как внутренних, так и внешних факторов. В этих обстоятельствах полагаем, что наличие гибких механизмов ценообразования является одним из наиболее актуальных факторов для более органичного развития экономики в целом, а также отдельных составляющих. Исследована схема системы эконометрических моделей ценообразования (СЭМЦ) (рис. 22). Она состоит из четырех групп моделей (по степени сложности и конструкции). В первую группу включаются простые, но базовые модели ценообразования, которые выявляются на основе одного, двух, трех факторов. Причем, при их выявлении применяется именно явная функциональная зависимость.
Во вторую группу включаются модели средней сложности. Они, как правило, являются многофакторными в отличие от первых групп моделей, их исследование осуществляется путем применения различных функциональных зависимостей.
В третью группу отнесены модели повышенной сложности, их преимущество заключается в том, что на этом типе учитываются как внутренние, так и внешние факторы. Эти типы моделей более адекватные, но здесь многое зависит от профессиональной ориентированности специалистов, так как необходимо учитывать не только сложившуюся ситуацию, но и поведение системы в будущем в стратегическом плане.
В нумерации моделей принята следующая индексация: первый индекс слева означает номер группы моделей, второй справа - номер модели в группе, т.е. номера индексов слева и справа образуют адреса эконометрических моделей ценообразования.
Каждая из групп (Мn,k) - это подкомплекс моделей ценообразования. В частности, если речь идет о таких моделях, как М1, 2, то здесь можно выделить отдельные эконометрические модели ценообразования на основе ощущаемой ценности товара. Например, модели ценообразования с учетом качественных характеристик цельномолочной продукции, мясных продуктов, других товаров первой необходимости и т.д.
В зависимости от сложности конструкции модели первой группы вполне могут составить конкуренцию моделям второй, третьей и даже четвертой группы. Это происходит тогда, когда ситуация корректируется ввиду непредвиденных обстоятельств, т.е. из-за сложившихся обстоятельств и ситуации необходимо учитывать более трех факторов или более сложные конструкции построения моделей.
И все же модели первой группы являются базовыми, отправными, так как именно на их основе происходит выстраивание более сложных, суперсложных моделей ценообразования.
В настоящее время состояние разработки системы эконометрических моделей ценообразования такова, что часть из них находится в стадии разработки, поиска, а часть - в совершенствовании.
ЭМЦ следует постоянно совершенствовать. Необходимо, чтобы ЭМЦ пополнялись новыми, более прогрессивными моделями, однако при этом должна быть выдержана общая методология ценообразования, обеспечивающая поступательное динамическое развитие экономики в целом, а также отдельных составляющих.
| Наименование подкомплекса моделей ценообразования | Группы эконометрических моделей по степени сложности и конструкции построения | |||
| I. простые модели (базовые) | II. модели средней сложности | III. модели повышенной степени сложности | IV. суперсложные модели | |
| 1. Базовые типовые модели ценообразования | 
| |||
| 2. Модели ценообразования на основе ощущаемой ценности товара | ||||
| 3. Модели ценообразования на основе текущих цен | ||||
| 4. Модели ценообразования на основе закрытых торгов | ||||
| 5. Модели ценообразования по методу "средние издержки плюс прибыль" | ||||
| 6. Модели ценообразования на основе анализа безубыточности и обеспечения целевой прибыли | ||||
| 7. Модели ценообразования на новый товар | ||||
| 8. Модели ценообразования в рамках товарного ассортимента |
Рис. 22. Схема системы эконометрических моделей
ценообразования
Продолжение схемы
| 9. Модел ценообразования по государственному принципу | 
| |||||
| 10. Модели ценообразования со скидками | ||||||
| 11. Модели ценообразования для стимулирования сбыта | ||||||
| 12. Модели обоснования дискриминационные цен | ||||||
| 13. Модели инициативного изменения цен (инициативное снижение, повышение, реакция потребителей, конкурентов, фирмы на изменение цен) | ||||||
| 14. Прочие необозначенные модели ценообразования | ||||||
| 15. Неопределенные модели ценообразования | ||||||
| 16. Новые ожидаемые прогрессивные модели ценообразования | ||||||
2.5. Оценка уравнения регрессии и корреляции
Для оценки существенности параметров регрессии и корреляции необходимо вспомнить математическую статистику. Как правило, сначала формируется нулевая гипотеза (Н0), т.е. осуществляется F- тест. Для этого необходимо сравнить (Fфакт) и (Fтабл.) . Значений F -критерия Фишера (Fтабл) определяется на основе следующей зависимости:
Fфакт. = 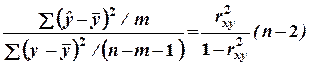 ,
,
где n - число единиц совокупности;
m - число параметров при переменных.
Fтабл. - это максимально возможное значение критерия под влиянием случайных факторов при данных степенях свободы.
Если Fтабл. < Fфакт., то (Н0) - гипотеза о случайной природе оцениваемых характеристик отклоняется.
Если Fтабл. > Fфакт., то гипотеза (Н0) не отклоняется.
Для оценки статистической значимости коэффициентов регрессии и корреляции рассчитываются t - критерий Стьюдента и доверительные интервалы каждого из показателей. Оценка коэффициентов регрессии и корреляции с помощью t -критерия Стьюдента производится путем сопоставления их значений с величиной случайной ошибки:
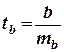 ;
; 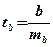 ;
; 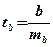 .
.
Случайные ошибки параметров линейной регрессии и коэффициента корреляции определяются по формулам:
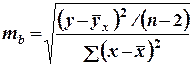 ;
;
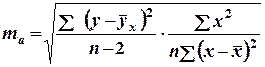 ;
;
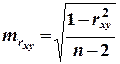 .
.
Сравнивая фактическое и критическое (табличное) значения t -статистика - tтабл., tфакт . принимаем или отвергаем гипотезу (Н0).
Если Fтабл. < Fфакт., то (Н0) отклоняется, т.е. а, b и rху сформировались под влиянием систематически действующего фактора х.
Если Fтабл. > Fфакт ., то гипотеза (Н0) не отклоняется и признается случайная природа формирования а, b, rху.
Для расчета доверительного интервала определяется предельная ошибка Δ для каждого показателя:
Δа = tтабл. ma, Δb = tтабл. mb.
Формулы для расчета доверительных интервалов имеют вид:
γа = а ± Δа; γа min = а - Δа; γа mах = а + Δа;
γb = b ± Δb; γаb min = b - Δb; γb mах = b + Δb.
Связь между F критерием Фишера и t -статистикой Стьюдента выражается равенством
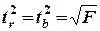 .
.
 2014-02-01
2014-02-01 956
956








