Теоретические вопросы к защите курсовой работы

Основные понятия векторной алгебры; примеры решения задач.

Задание 2

Задание №1

Заданы вершины треугольника АВС. Координаты точек заданы в таблице. Найти: 1) длину стороны АВ; 2) уравнения сторон треугольника и их угловые коэффициенты; 3) внутренний угол А; 4) уравнение высоты СД и ее длину; 5) уравнение медианы АЕ и ее длину; 6) периметр треугольника. Построить чертеж.

№ задачи	А	В	С	№ задачи	А	В	С
1.01	(-5;0)	(7;9)	(5;-5)	1.18	(-4;1)	(8;-8)	(6;6)
1.02	(-7;2)	(5;11)	(3;-3)	1.19	(-7;-1)	(-5;-10)	(3;4)
1.03	(-5;-3)	(7;3)	(5;-8)	1.20	(-3;3)	(9;-6)	(7;8)
1.04	(-6;-2)	(6;7)	(4;-7)	1.21	(-2;1)	(10;10)	(8;-4)
1.05	(-8;-4)	(4;5)	(2;-9)	1.22	(-4;-1)	(8;8)	(6;-6)
1.06	(0;-1)	(12;8)	(10;-4)	1.23	(-1;0)	(11;9)	(9;-3)
1.07	(-6;1)	(6;10)	(4;-4)	1.24	(-3;-3)	(9;6)	(7;-8)
1.08	(-2;-4)	(10;5)	(8;-9)	1.25	(-3;0)	(9;9)	(7;-5)
1.09	(-3;0)	(9;9)	(7;-5)	1.26	(1;4)	(13;-5)	(11;9)
1.10	(-9;-2)	(3;7)	(1;-7)	1.27	(1;1)	(7;4)	(4;5)
1.11	(-5;2)	(7;-7)	(5;7)	1.28	(1;1)	(-5;4)	(-2;5)
1.12	(-7;5)	(5;-4)	(3;10)	1.29	(-1;1)	(5;4)	(2;5)
1.13	(-7;1)	(5;-8)	(3;6)	1.30	(-1;1)	(-7;4)	(-4;5)
1.14	(0;3)	(12;-6)	(10;8)	1.31	(1;-3)	(-3;2)	(-3;-3)
1.15	(-8;4)	(4;-5)	(2;9)	1.32	(1;-1)	(4;5)	(-1;3)
1.16	(-2;2)	(10;-7)	(8;7)	1.33	(7;1)	(-5;3)	(3;3)
1.17	(1;2)	(13;-7)	(11;7)	1.34	(-2;3)	(2;-3)	(2;2)

Найти каноническое уравнение прямой, проходящей через точку А4, перпендикулярно плоскости, проходящей через точки А1, А2, А3. Построить плоскость и прямую.

№	А1	А2	А3	А4
1.01	0,0,2	2,0,5	1,1,0	4,1,2
1.02	3,0,5	0,0,2	4,1,2	1,1,0
1.03	1,1,0	4,1,2	0,0,2	3,0,5
1.04	4,1,2	1,1,0	3,0,5	0,0,2
1.05	0,0,0	3,-2,1	1,4,0	5,2,3
1.06	3,1,0	0,7,2	-1,0,-5	4,1,5
1.07	1,-1,1	0,2,4	1,3,3	4,2,-3
1.08	1,-1,2	2,1,1	1,1,4	0,0,0
1.09	1,-3,2	5,1,-4	2,0,3	1,-5,2
1.10	3,5,3	-2,11,-5	1,2,4	0,6,4
1.11	2,0,5	1,1,0	4,1,2	0,0,2
1.12	0,0,2	4,1,2	1,1,0	3,0,5
1.13	4,1,2	0,0,2	3,0,5	1,1,0
1.14	1,1,0	3,0,5	0,0,2	4,1,2
1.15	3,-2,1	1,4,0	5,2,3	0,0,0
1.16	0,7,2	-1,0,-5	4,1,5	3,1,0
1.17	0,2,4	1,3,3	4,2,-3	1,-1,1
1.18	2,1,1	1,1,4	0,0,0	1,-1,2
1.19	5,1,-4	2,0,3	1,-5,2	1,-3,2
1.20	-2,11,-5	1,2,4	0,6,4	3,5,3
1.21	1,1,0	4,1,2	0,0,2	2,0,5
1.22	4,1,2	1,1,0	3,0,5	0,0,2
1.23	0,0,2	3,0,5	1,1,0	4,1,2
1.24	3,0,5	0,0,2	4,1,2	1,1,0
1.25	1,4,0	5,2,3	0,0,0	3,-2,1
1.26	-1,0,-5	4,1,5	3,1,0	0,7,2
1.27	1,3,3	4,2,-3	1,-1,1	0,2,4
1.28	1,1,4	0,0,0	1,-1,2	2,1,1
1.29	2,0,3	1,-5,2	1,-3,2	5,1,-4
1.30	1,2,4	0,6,4	3,5,3	-2,11,-5

Основные понятия включают в себя: понятие вектора, разложение вектора по другим векторам, модуль вектора, скалярное произведение, векторное произведение и смешанное произведение, а также их приложения для решения задач.

Пример 1. Задание. Разложить вектор 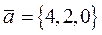по векторам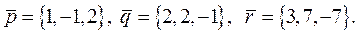

Прежде чем привести решение задачи напомним понятие линейной зависимости системы векторов.

Рассмотрим систему векторов 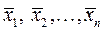и составим равенство вида:

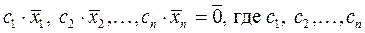– постоянные величины. Если это равенство выполняется только при одновременном равенстве нулю всех ,

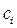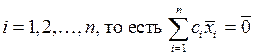, тогда система векторов называется линейно независимой, в противном случае – система векторов линейно зависима, то есть один вектор можно представить в виде линейной комбинации других векторов.

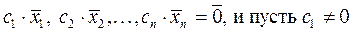. Разделим левую и правую части равенства на 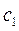, получим:

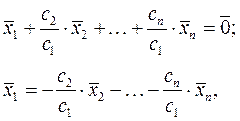
то есть вектор 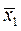представлен в виде линейной комбинации .

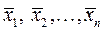Решение.

Разложить вектор 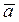по векторам 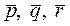это значит представить его в виде линейной комбинации 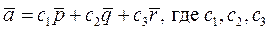– искомые числа.

Представим линейную комбинацию в координатной форме

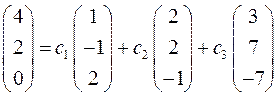
И получим систему линейных уравнений

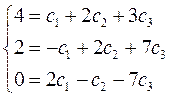
Решение системы имеет вид: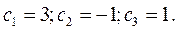

Следовательно: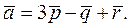

Пример 2.

Напомним понятие длины вектора (модуля вектора)

Если 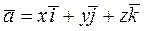, то

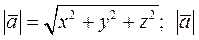– называется длиной вектора.

Рассмотрим свойство скалярного произведения: 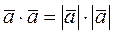, то есть .

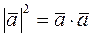Задание.

Найти длину вектора 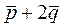, если

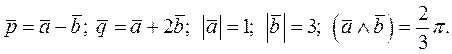
Решение. Имеем

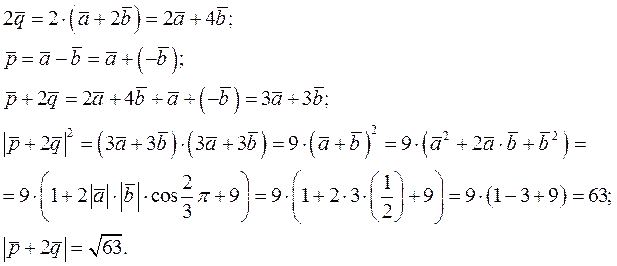
Пример 3.

Напомним определение коллинеарности двух векторов 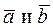отличных от нуля: два вектора 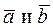называются коллинеарными, если 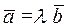, где 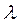– некоторый постоянный множитель.

Задание.

Найти вектор 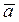, коллинеарный вектору 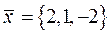и удовлетворяющий условию: скалярное произведение векторов .

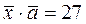Решение.

Запишем условие коллинеарности двух векторов 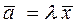и полученный вектор 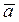подставим в условие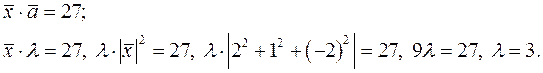

Следовательно .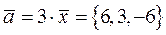

Пример 4.

Напомним определение скалярного произведения векторов:

.

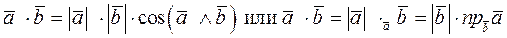Задание.

Вычислить проекцию вектора 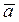на направление вектора 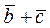, если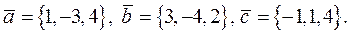

Решение.

Обозначим 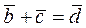, тогда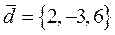

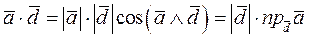, отсюда

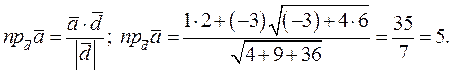
Ответ:

Пример 5.

Пусть 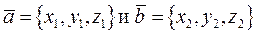. Напомним, что векторное произведение двух векторов 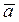и 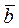равно: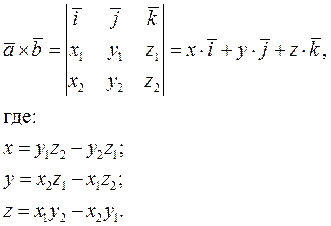

Модуль векторного произведения равен площади параллелограмма, построенного на этих векторах.

Задание.

Найти площадь треугольника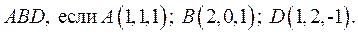

Решение.

Построим параллелограмм 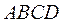на векторах 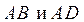(рис. 1):

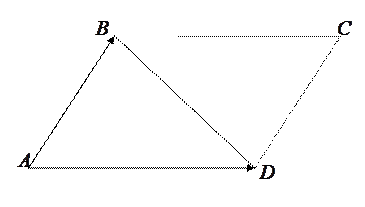
рис. 1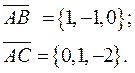

Пример 6.

Задание.

Найти вектор 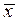, перпендикулярный векторам 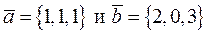и образующий с осью 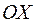тупой угол, если .

Решение.

Если 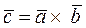, тогда вектор 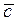перпендикулярен векторам .

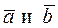Найдем вектор :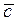

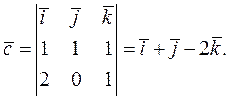
Так как 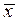тоже перпендикулярен 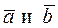, следовательно вектора 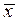и 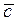- коллинеарны. Запишем условие коллинеарности векторов: ,

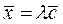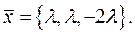
По условию 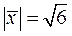, то есть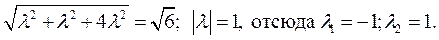

Так как вектор 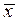образует с осью 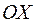тупой угол, то его проекция на ось 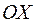должна быть отрицательной.

Отсюда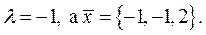

Пример 7.

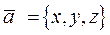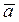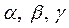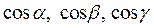Рассмотрим вектор . Вектор образует с осями координат углы , а называются направляющими косинусами, при этом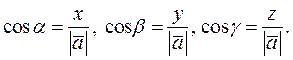

Задание.

Найти направляющие косинусы вектора силы 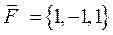, приложенной в точке 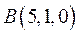, и момент этой силы относительно точки .

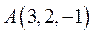Решение.

Найдем направляющие косинусы вектора силы:

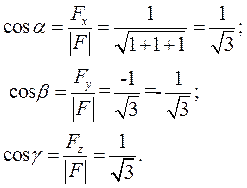
Момент силы определим как векторное произведение вектора 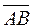на вектор 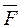. Имеем

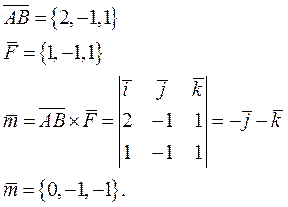
Пример 8.

Напомним формулу смешанного произведения трех векторов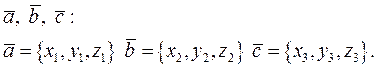

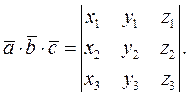
Известно, что модуль смешанного произведения 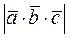равен объему параллелепипеда, построенного на этих векторах.

Задача.

Найти длину высоты пирамиды, опущенной из вершины 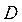(рис. 2), если ее вершины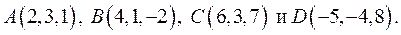

Решение.

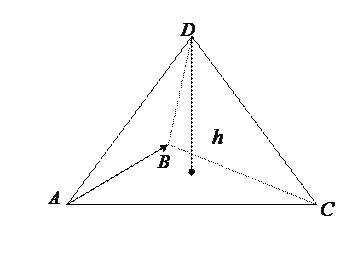
рис. 2

Найдем векторы:

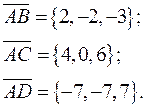
Объем пирамиды, построенной на векторах 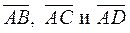, равен одной шестой модуля смешанного произведения этих векторов.

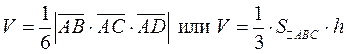, где 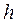– высота пирамиды, а площадь прямоугольника, построенного на векторах 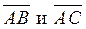равна одной второй векторного произведения .

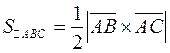Вычислим смешанное произведение векторов

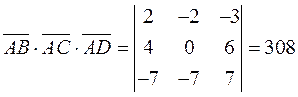
Отсюда 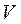пирамиды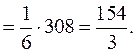

Вычислим векторное произведение векторов:

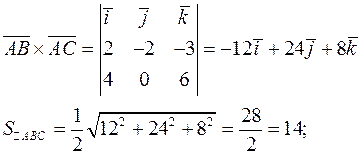
Найдем высоту пирамиды:

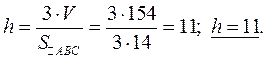
1. Определение вектора. Линейные операции над векторами, свойства этих операций.

2. Разложение вектора по двум векторам на плоскости. Доказать возможность и единственность такого разложения.

3. Разложение вектора по трем векторам в пространстве.

4. Проекции вектора на ось. Свойства проекции.

5. Разложение вектора по координатным ортам. Координаты вектора. Направляющие векторы, вывод формулы .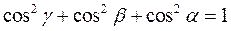

6. Условия коллинеарности и компланарности векторов в векторной и координатной форме.

7. Радиус-вектор точки. Модуль вектора. Расстояние между двумя точками.

8. Вывод формулы деления отрезка в данном отношении.

9. Скалярное произведение векторов, его физическое толкование. Свойства скалярного произведения.

10. Проекция вектора на вектор. Угол между векторами. Необходимое и достаточное условие перпендикулярности векторов.

11. Скалярное произведение векторов в координатной форме.

12. Векторное произведение двух векторов, его физическое толкование.

13. Векторное произведение векторов в координатной форме.

14. Геометрические приложения векторного произведения.

15. Свойства векторного произведения.

16. Смешанное произведение трех векторов в координатной форме.

17. Необходимое и достаточное условие компланарности векторов.

18. Смешанное произведение векторов в координатной форме.

19. Свойства смешанного произведения.