Для более серьёзной оценки уровня смертности используются, как отмечалось, возрастные коэффициенты. Однако их много. Рассчитать суммарный коэффициент смертности (по аналогии с суммарным коэффициентом рождаемости) нельзя. Компенсировать трудности анализа возрастных коэффициентов позволяет индексный метод.
Для этого представим общий коэффициент смертности как среднее арифметическое из возрастных коэффициентов смертности:
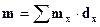 ,(5.5)
,(5.5)
где: 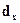 – доля умерших в возрасте "x" во всей совокупности.
– доля умерших в возрасте "x" во всей совокупности.
Данная формула позволяет проанализировать структуру населения по признаку смертности.
Сравнение общих коэффициентов смертности в динамике через их соотношение будет иметь следующий вид:
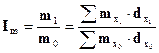 (5.6)
(5.6)
Сделаем некоторые преобразования:
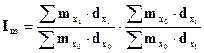 (5.7)
(5.7)
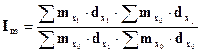 (5.8)
(5.8)
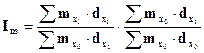 (5.9)
(5.9)
где: 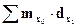 – общий коэффициент в отчётном периоде при условии, что возрастные коэффициенты смертности остались на базисном уровне, а изменилась только возрастная структура.
– общий коэффициент в отчётном периоде при условии, что возрастные коэффициенты смертности остались на базисном уровне, а изменилась только возрастная структура.
Таким образом, получили взаимосвязь индексов:
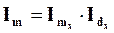 , (5.10)
, (5.10)
где 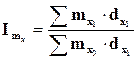 – индекс постоянного состава, характеризующий изменение общего коэффициента смертности под влиянием изменения возрастных коэффициентов смертности; (5.11)
– индекс постоянного состава, характеризующий изменение общего коэффициента смертности под влиянием изменения возрастных коэффициентов смертности; (5.11)
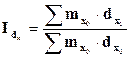 – индекс структурных сдвигов, характеризующий изменение общего коэффициента смертности под влиянием изменения возрастной структуры. (5.12)
– индекс структурных сдвигов, характеризующий изменение общего коэффициента смертности под влиянием изменения возрастной структуры. (5.12)
Эту же взаимосвязь индексов можно представить следующим образом:
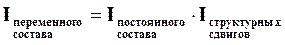 (5.13)
(5.13)
Для нахождения абсолютного влияния факторов на изменение общего коэффициента смертности требуется из числителя соответствующего индекса вычесть знаменатель:
- абсолютное влияние изменения возрастных коэффициентов смертности:
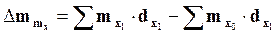 ; (5.14)
; (5.14)
- абсолютное влияние изменения возрастной структуры:
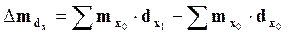 ; (5.15)
; (5.15)
- абсолютное влияние изменения двух факторов вместе:
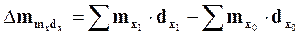 (5.16)
(5.16)
Задание 5.1. По данным таблицы 5.1требуется определить:
1.Общие коэффициенты смертности для всего населения в базисном и отчётном периодах.
2. Индекс общего коэффициента смертности.
3. Индекс коэффициентов смертности постоянного состава.
4. Индекс, характеризующий влияние структурных сдвигов на динамику среднего (общего) коэффициента смертности.
Таблица 5.1
Динамика возрастных коэффициентов смертности*
| Возраст, лет | Базисный период | Отчётный период | ||
коэффициент смертности, %о
| удельный вес возрастных групп в общей численности населения, % | коэффициент смертности, %о | удельный вес возрастных групп в общей численности населения, % | |
| до 50 | ||||
| 50 и старше |
*Исходные данные условные.
Решение:
1. Общие коэффициенты смертности для всего населения базисного и отчётного периода (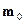 и
и 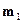 ) определим по формуле 5.5:
) определим по формуле 5.5:
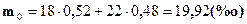
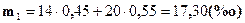
2. Индекс общего коэффициента смертности рассчитаем по формуле 5.6:
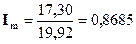 (или 86,85%), т.е. общий коэффициент смертности в отчётном периоде по сравнению с базисным периодом сократился на 13,15% (86,85% – 100%).
(или 86,85%), т.е. общий коэффициент смертности в отчётном периоде по сравнению с базисным периодом сократился на 13,15% (86,85% – 100%).
3. Индекс коэффициентов смертности постоянного состава рассчитаем по формуле 5.11:
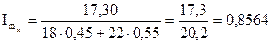 (или 85,64%), т.е. общий коэффициент смертности в отчётном периоде по сравнению с базисным периодом под влиянием снижения возрастных коэффициентов смертности
(или 85,64%), т.е. общий коэффициент смертности в отчётном периоде по сравнению с базисным периодом под влиянием снижения возрастных коэффициентов смертности
сократился на 14,36% (85,64% - 100%).
4. Индекс структурных сдвигов рассчитаем по формуле 5.12:
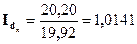 (или 101,41%), т.е. общий коэффициент смертности в отчётном периоде по сравнению с базисным периодом под влиянием увеличения доли старшей группы населения во всём населении вырос на 1,41% (101,41% - 100%).
(или 101,41%), т.е. общий коэффициент смертности в отчётном периоде по сравнению с базисным периодом под влиянием увеличения доли старшей группы населения во всём населении вырос на 1,41% (101,41% - 100%).
В качестве проверки используем взаимосвязь индексов (формула 5.10):
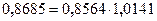
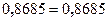
 2013-12-31
2013-12-31 787
787








