Таблица 5.6
Таблица 5.5 Стандартные коэффициенты рождаемости, %о
| Возраст | Гуттериты | ГМЕР | Россия, 1998 |
| 15-19 | - | ||
| 20-24 | |||
| 25-29 | |||
| 30-34 | 33.4 | ||
| 35-39 | 11.5 | ||
| 40-44 | 2.3 | ||
| 45-49 | 0.1 |
Здесь В - годовое число рождений; ASFRX - наблюдаемые повозрастные коэффициенты рождаемости; Fx - среднегодовая численность женщин возраста x;ASFRs - повозрастные коэффициенты рождаемости стандарта (гуттеритов).
Индекс брачной рождаемости (Ig) равен отношению наблюдаемого числа рождений в браке к ожидаемому при условии, что реальное население имеет те же повозрастные показатели брачной рождаемости, что и стандарт естественной рождаемости:
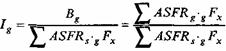
где Bg - годовое наблюдаемое число брачных рождений (Bg = ASFRggFx); ASFRg - наблюдаемые повозрастные коэффициенты брачной рождаемости; gFx - численность женщин возраста х, состоящих в браке; ASFRS - повозрастные коэффициенты рождаемости стандарта (гуттеритов).
Индекс внебрачной рождаемости (Ih) равен отношению наблюдаемого числа рождений вне брака к ожидаемому при условии, что реальное население имеет повозрастные показатели внебрачной рождаемости, равные стандарту естественной рождаемости:
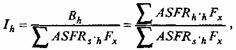
где Bh - годовое наблюдаемое число внебрачных рождений (Bh = ASFRh-hFx); ASFRh - наблюдаемые повозрастные коэффициенты внебрачной рождаемости; hFx - численность женщин возраста х, не состоящих в браке; ASFRs - повозрастные коэффициенты рождаемости стандарта (гуттеритов1
Индекс брачной структуры равен отношению ожидаемого числа брачных рождений к ожидаемому числу всех рождений:
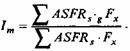
Это выражение можно представить иначе
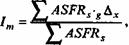
где gx - доля женщин возрастах, состоящих в браке, равная g Fx/Fx
Иначе говоря, индекс брачной структуры равен средневзвешенной доле женщин репродуктивного возраста, состоящих в браке, причем весами выступают повозрастные коэффициенты стандарта естественной рождаемости. Это позволяет легко рассчитывать индекс Im, зная лишь повозрастные доли замужних женщин.
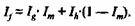
Если же внебрачная рождаемость отсутствует, т. е. Ih = 0, то это соотношение равно:
Поскольку Б = Bg + Bh и Fx = gFx + hFx, индексы рождаемости связаны между собой следующим соотношением:
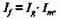
В табл. 5.6 приведен пример расчета индексов Коула для населения России (1994 г.). Как видно из таблицы, население России использует максимальный потенциал рождаемости менее, чем на 10%.
Гипотетический минимум естественной рождаемости Российский демограф В.А. Борисов, разрабатывая свой вариант нормативного подхода, исходил из того, что использовать рождаемость гуттеритов в качестве стандарта естественной рождаемости методологически неправильно из-за уникальности этого субнаселения. По его мнению, таким стандартом может быть только стандарт, разработанный на основе математической модели репродуктивного процесса, так как только в этом случае можно «использовать массовые фактические данные». По мнению В.А. Борисова, более правильно определять не максимум, а минимум естественной рождаемости, чтобы быть уверенным, что уровень естественной брачной рождаемости не опустится ниже этого минимума в нормальных санитарных условиях. Поэтому в упомянутой математической модели надо брать такие значения ее параметров, которые находились бы в пределах санитарной нормы и были бы в ее пределах наименее благоприятными.
| Возраст | Стандарт естественной рождаемости (гуттери-ты), на 1 женщину | Численность женщин, всего (тысяч) | Доля женщин, состоящих в браке | Ожидаемое число всех рождений, (тысяч) | Ожидаемое число рождений в браке, (тысяч) | Ожидаемое число внебрачных рождений (тысяч) | Расчёт индекса брачной структуры |
| 4. | 5 = (2)*(З) | 6 = (3)*(2)*(4) | 7 = (5)-(6) | 8 = (2)*(4) | |||
| 15-19 | 0,3 | 0,138 | 0,0414 | ||||
| 20-24 | 0,55 | 0,565 | 0,31075 | ||||
| 25-29 | 0,502 | 0,751 | 0,377002 | ||||
| 30-34 | 0,447 | 0,798 | 0,356706 | ||||
| 35-39 | 0,406 | 0,796 | 0,323176 | ||||
| 40-44 | 0,222 | 0,77 | 0,17094 | ||||
| 45-49 | 0,061 | 0,737 | 0,044957 | ||||
| всего | 2,488 | 1,624931 | |||||
| Родилось в 1994 г. | |||||||
| Индекс общей рождаемости | 0,104 | ||||||
| Индекс брачной рождаемости | 0,090 | ||||||
| Индекс внебрачной рождаемости | 0,065 | ||||||
| Индекс брачной структуры | 0,653 |
Исходя из этих предпосылок, В.А. Борисов производит расчет показателя брачной рождаемости для возраста 20- 24 года. В результате он получил значение повозрастного коэффициента рождаемости для этого возраста, равное 400%о. Для более старших возрастов он отступил от моделирования репродуктивного процесса, применив, подобно Л. Анри, усреднение показателей повозрастной рождаемости для 8 реальных населений, у которых величина ASFR20 24 достоверно превышает 400%о, нормализацию ASFR для более старших возрастов относительно возраста 20-24 года, а также преобразование модельного значения ASFR20 24 в повозрастные показатели рождаемости с помощью этих коэффициентов нормализации25.
В результате этой многоступенчатой процедуры В.А. Борисов получил свой стандарт естественной рождаемости, названный им «гипотетическим минимумом естественной рождаемости», или ГМЕР (табл. 5.7). По мнению В.А. Борисова, повозрастная рождаемость не может быть ниже этих значений, если отсутствуют какие-либо экстремальные обстоятельства.
Относительно внебрачной рождаемости и в возрастах моложе 20 лет и старше 49 лет, В.А. Борисов полагал, что «наиболее верным представляется оставить фактическое число неизменным (т. е. считать, что число родившихся вне брака и у матерей моложе 20 лет и старше 49 лет в условиях естественной рождаемости было бы таким же, каким оно и есть фактически)»26.
Затем, используя показатели повозрастной рождаемости стандарта и фактические данные о возрастной структуре женщин репродуктивного возраста, рассчитываются ожидаемые значения абсолютного числа рождений и общего коэффициента рождаемости, которые сопоставляются с фактическими. Разница между ожидаемыми и фактическими значениями характеризует степень реализации ГМЕР, масштабы распространенности среди населения намеренного ограничения рождаемости, роль поведенческой компоненты рождаемости и вклад репродуктивного поведения в ее уровень27.
 2013-12-31
2013-12-31 708
708








