Алгоритм определения наибольшего (наименьшего) числа
Дан: ряд произвольных чисел 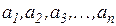 .
.
Определить: наибольшее число amax и его место в ряде k.
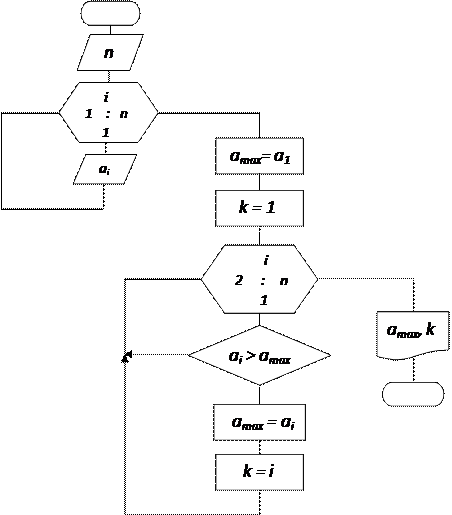
Типовой алгоритм для решения таких задач приведен на рис.8.3.
Он основан на использовании циклической операции, в которой поочередно производится сравнение всех чисел ряда с числом 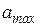 , играющим
, играющим
роль эталона для сравнения. В качестве начального значения 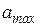 выбирается первый элемент ряда
выбирается первый элемент ряда 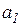 независимо от его истинного значения (наибольшее, наименьшее среди чисел ряда или какое-либо другое).
независимо от его истинного значения (наибольшее, наименьшее среди чисел ряда или какое-либо другое).
Переменная 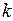 предназначена для хранения текущего адреса максимального числа, на старте этот адрес – единица. Параметр цикла
предназначена для хранения текущего адреса максимального числа, на старте этот адрес – единица. Параметр цикла 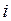 , как и в предыдущих алгоритмах, определяет адрес (порядковый номер) числа ряда и имеет начальное значение 2, так, как первое число уже использовано в роли amax. Далее выполняется сравнение значения текущего числа ряда
, как и в предыдущих алгоритмах, определяет адрес (порядковый номер) числа ряда и имеет начальное значение 2, так, как первое число уже использовано в роли amax. Далее выполняется сравнение значения текущего числа ряда 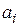 , имеющего адрес
, имеющего адрес 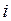 , с числом, выполняющим на данный момент роль максимального amax. Если в результате сравнения текущее число
, с числом, выполняющим на данный момент роль максимального amax. Если в результате сравнения текущее число 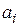 окажется большим максимального
окажется большим максимального 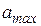 , то с этого момента роль максимального будет выполнять текущее число ai, а его адрес будет зафиксирован в качестве значения переменной
, то с этого момента роль максимального будет выполнять текущее число ai, а его адрес будет зафиксирован в качестве значения переменной 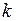 . Если же результат сравнения будет иным, то никакие изменения не происходят, а сразу выполняется продвижение цикла, то есть устанавливается адрес i следующего числа ряда и производится переход к новому выполнению тела цикла. В результате перебора всех чисел ряда, определяется наибольшее число
. Если же результат сравнения будет иным, то никакие изменения не происходят, а сразу выполняется продвижение цикла, то есть устанавливается адрес i следующего числа ряда и производится переход к новому выполнению тела цикла. В результате перебора всех чисел ряда, определяется наибольшее число 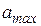 , его адрес
, его адрес 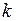 , и их значения выводятся на экран.
, и их значения выводятся на экран.
Определение наименьшего числа осуществляется аналогично. Для этого в представленном алгоритме (рис.8.3) идентификатор 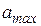 следует заменить
следует заменить 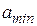 (поскольку этот идентификатор будет отвечать назначению алгоритма) и операцию сравнения
(поскольку этот идентификатор будет отвечать назначению алгоритма) и операцию сравнения 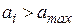 заменить операцией
заменить операцией 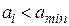 .
.
 |
_
Рис. 8.3 Блок – схема определения наибольшего числа ряда
 2014-01-24
2014-01-24 734
734








