Определение линии пересечения поверхностей с помощью вспомогательных сферических поверхностей

Вспомогательные сферические поверхности применяются, когда оси поверхностей вращения пересекаются друг с другом и параллельны какой-либо плоскости проекций.

Метод основывается на известном свойстве:
"Две любые соосные поверхности вращения пересекаются по окружностям, проходящим через точки пересечения меридианов поверхностей".

Плоскости окружностей сечения перпендикулярны оси поверхности вращения, а центры окружностей принадлежат этой оси. Поэтому, если оси поверхностей вращения параллельны плоскости проекции, то на эту плоскость окружности сечения проецируются в отрезки прямых, перпендикулярных проекциям оси вращения.

В качестве вспомогательной секущей поверхности вращения используют сферу, т.к. её просто вычертить.

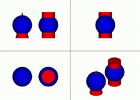Рис.9

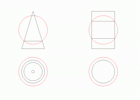Рис.10

Пример. Дано: 2 поверхности вращения - цилиндр и конус, оси которых пересекаются и параллельны плоскости проекций V.

Нужно: Найти (построить) линию пересечения этих поверхностей вращения с помощью вспомогательных концентрических сфер.

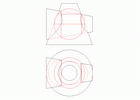
Точки, наиболее удалённые от оснований малого конуса, найдём, вписав сферу в большой конус.

Проекции линии пересечения представляют собой кривые 2-го порядка. Это следует из теоремы:
"Если пересекающиеся поверхности 2-го порядка имеют общую плоскость симметрии, то линии их пересечения проецируются на эту плоскость (или параллельную ей) в кривую 2-го порядка."

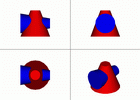Рис.11