Определение 6. Произведением ненулевого вектора  на отличное от нуля действительное число a называется такой вектор
на отличное от нуля действительное число a называется такой вектор  (обозначение
(обозначение 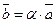 ), что
), что
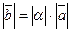 ,
,

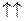
 , если a > 0,
, если a > 0,

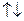
 , если a < 0.
, если a < 0.
Если 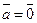 или a = 0, то вектор
или a = 0, то вектор  считается равным нулевому вектору.
считается равным нулевому вектору.
Свойства операции умножения вектора на действительное число.
10. Произведение любого вектора на любое действительное число определено и однозначно.
20. 1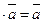 для любого вектора
для любого вектора  .
.
30. 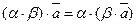 для любого вектора
для любого вектора  и любых действительных чисел a, b.
и любых действительных чисел a, b.
Доказательство. Возможны случаи.
1) a = 0, или b = 0, или  =
= 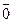 . В этом случае равенство очевидно.
. В этом случае равенство очевидно.
2) a ¹ 0, b ¹ 0 и  ¹
¹ 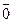 . Сравним длины и направления векторов, стоящих в левой и правой частях доказываемого равенства.
. Сравним длины и направления векторов, стоящих в левой и правой частях доказываемого равенства.
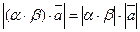 ,
,
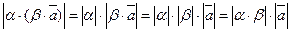 .
.
Следовательно, 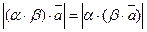 . Так как направления векторов зависят от знаков коэффициентов, то рассмотрим все возможные случаи.
. Так как направления векторов зависят от знаков коэффициентов, то рассмотрим все возможные случаи.
а) a и b одного знака (пусть a > 0, b > 0). В этом случае a × b > 0.
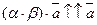 ,
,
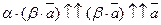 , следовательно,
, следовательно, 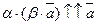 .
.
Итак, левая и правая части доказываемого равенства имеют одинаковые длины и направления, поэтому они равны.
б) a и b имеют разные знаки (пусть a > 0, b < 0). В этом случае a × b < 0.
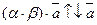 .
.
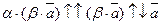 .
.
Снова получили, что левая и правая части доказываемого равенства имеют одинаковые длины и направления, поэтому они равны.
40. 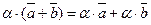 и (
и (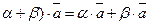 для любых векторов
для любых векторов  ,
,  и любых действительных чисел a, b. (Докажите это свойство самостоятельно).
и любых действительных чисел a, b. (Докажите это свойство самостоятельно).
 2014-01-25
2014-01-25 991
991








