Определение 1. Геометрический отрезок называется ориентированным, если указан порядок его концов.
Определение 2. Вектором (геометрическим вектором) называется ориентированный отрезок. При этом начало и конец ориентированного отрезка называются соответственно началом и концом вектора. Длина ориентированного отрезка называется длиной вектора.
Вектор обозначается 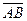 , где А – начало, а В – конец вектора. Если начало и конец вектора нас не интересуют, то вектор обозначают
, где А – начало, а В – конец вектора. Если начало и конец вектора нас не интересуют, то вектор обозначают  . Длина вектора обозначается
. Длина вектора обозначается 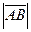 или
или 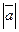 . Если начало и конец вектора совпадают, то вектор называют нулевым и обозначают
. Если начало и конец вектора совпадают, то вектор называют нулевым и обозначают 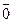 . Если начало и конец вектора – различные точки (А ¹ В), то существует и только один луч с началом А, проходящий через точку В. Этот луч задаёт в пространстве направление, которое называется направлением данного вектора. Нулевой вектор не имеет направления.
. Если начало и конец вектора – различные точки (А ¹ В), то существует и только один луч с началом А, проходящий через точку В. Этот луч задаёт в пространстве направление, которое называется направлением данного вектора. Нулевой вектор не имеет направления.
Определение 3. Два вектора называются равными, если они либо оба нулевые, либо имеют одинаковые длину и направление.
Равенство векторов обладает следующими очевидными свойствами: 1) рефлексивность (всякий вектор равен сам себе); 2) симметричность (если 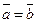 , то
, то 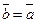 ); 3) транзитивность (если
); 3) транзитивность (если 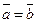 и
и 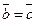 , то
, то 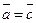 ).
).
Множество всех равных векторов можно задать 1) одним из векторов (ориентированным отрезком); 2) упорядоченной парой точек; 3) длиной и направлением (в случае ненулевого вектора).
Пусть даны вектор  и точка А. Если и точка А. Если 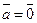 , то существует и только один вектор с началом в точке А, равный данному вектору. Это вектор , то существует и только один вектор с началом в точке А, равный данному вектору. Это вектор 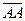 (т.е. В = А). Если (т.е. В = А). Если 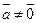 , то существует и только один луч, сонаправленный с вектором , то существует и только один луч, сонаправленный с вектором  . На этом луче существует и только одна точка В, расстояние от которой до точки А равно . На этом луче существует и только одна точка В, расстояние от которой до точки А равно 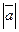 . Но тогда . Но тогда 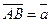 | 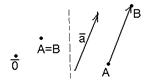 Рис. 1 Рис. 1 |
(рис. 1). Будем говорить, что вектор  отложен от точки А. Итак, любой вектор можно отложить от любой точки и только единственным образом.
отложен от точки А. Итак, любой вектор можно отложить от любой точки и только единственным образом.
 2014-01-25
2014-01-25 1262
1262








