Сущность метода и основные понятия

Аксонометрическая проекция, или аксонометрия есть параллельная проекция фигуры-оригинала и осей координат пространства, к которым эта фигура отнесена на одну плоскость проекций, называемой аксонометрической плоскостью проекций (П¢ ).

Аксонометрическую проекцию получают по методу параллельного проецирования, поэтому все свойства параллельного проецирования остаются справедливыми и для аксонометрической проекции. Например, сохраняется параллельность прямых и пропорциональность деления отрезков.

Достоинством такой проекции является наглядность. Недостатком – проецирование на одну плоскость проекций.

Сущность метода рассмотрим на примере получения аксонометрии точки А. Выберем в пространстве прямоугольную систему координат Охуz и точку А, положение которой относительно осей координат определено: X_А=OA_X, Y_А=A_XA₁, Z_А=A₁A (см. рис.13.1). Полученная ломаная AA₁A_XO – координатная ломаная точки A. По каждому из направлений натуральной системы координат (хуz) отложим отрезки единичной длины e_X, e_Y, e_Z.

Спроецируем в направлении S на плоскость П¢ выбранную декартовую систему координат Охуz вместе с точкой А и ее горизонтальной (прямоугольной) проекцией А₁ на координатной плоскости хОу, а также единичные отрезки e_X, e_Y, e_Z.

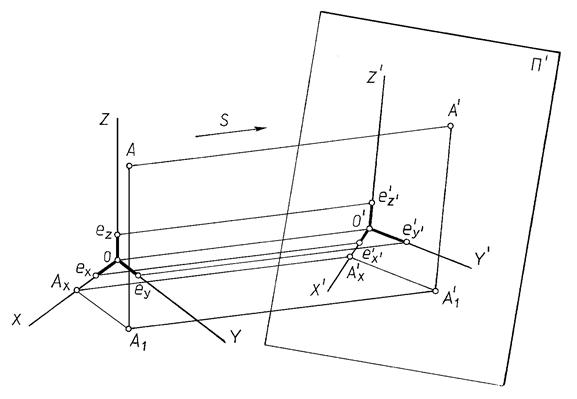
Рис.13.1

Оси О'x'y'z', полученные проецированием координатных осей пространства на аксонометрическую плоскость проекций П¢, называются аксонометрическими осями; проекция А¢, - аксонометрической проекцией точки А, а А₁ ¢, – вторичной проекцией точки А. А¢А₁¢А_х¢О¢ - аксонометрическая проекция координатной ломаной точки А.

Для получения обратимого чертежа в том случае, если проецирование ведется на одну плоскость проекций необходимо использовать вторичную проекцию. Вторичной проекцией называется аксонометрическое изображение не самой точки, а одной из ее ортогональных проекций (чаще всего горизонтальной). Этот термин хорошо подчеркивает тот факт, что проекция А₁^’ получается в результате двух последовательных проецирований. Заметим, что для получения наглядного аксонометрического изображения, направление проецирования S не должно быть параллельным ни одной из координатных осей (x,y,z) или координатной плоскости, так как при этом аксонометрическая проекция такой плоскости изобразится прямой линией, и чертеж утратит свою наглядность.

Если плоскость аксонометрических проекций П¢ не параллельна ни одной из координатных осей, то, очевидно, что любые отрезки, расположенные в пространстве на осях e_X, e_Y, e_Z (или параллельные осям), проецируются на плоскость П^’ с некоторым искажением e_X', e_Y', e_Z'. Отношение длины аксонометрической проекции отрезка, лежащего на координатной оси или параллельного ей, к истинной длине этого отрезка называется коэффициентом (показателем) искажения по соответствующей аксонометрической оси:

e_X' / e_X = m, e_Y' / e_Y = n, e_Z' / e_Z = k.

Числовое выражение коэффициентов искажения показывает, во сколько раз увеличиваются или уменьшаются отрезки по осям на аксонометрических изображениях. В зависимости от соотношения коэффициентов искажения аксонометрические проекции делятся на:

- изометрические, если коэффициенты искажения по всем трем осям равны m = n = k;

- диметрические, если коэффициенты искажения одинаковы лишь по двум осям, например, m = k ≠ n;

- триметрические, если все три показателя искажения разные

m ≠ n ≠ k.

В зависимости от угла j между направлением проецирования S и аксонометрической плоскостью проекций П¢ различают:

- прямоугольную аксонометрическую проекцию, если

j = S ^ П¢= 90°, и

- косоугольную аксонометрическую проекцию,если j = S ^ П¢≠ 90°.

Между коэффициентами искажения и углом j, образованным направлением проецирования S с плоскостью П¢, существует следующая зависимость:

m ²+n ²+k ²=2+ctg²j. (1)

Так в общем случае можно получить множество аксонометрических проекций, отличающихся друг от друга направлением аксонометрических осей и коэффициентами искажения по ним. Это положение сформулировано в 1851 году и доказано теоремой К. Польке, которая гласит: три отрезка произвольной длины, лежащие в одной плоскости и, выходящие из одной точки под произвольными углами друг к другу, представляют параллельную проекцию трёх равных отрезков, отложенных на прямоугольных осях координат от начала.

Позже Г.Шварц обобщил теорему К. Польке, которая имеет существенное значение, как для теории аксонометрии, так и для многих её приложений. На основании теоремы Польке системы аксонометрических осей, а также отношение коэффициентов искажения по ним, могут быть заданы совершенно произвольно. При произвольном выборе характеристических данных, определяющих аксонометрическую систему, получается косоугольная триметрическая проекция общего вида.

Однако из многих систем аксонометрических проекций на практике чаще всего пользуются теми, которые рекомендует ГОСТ 2.317-69 «Аксонометрические проекции», а именно: прямоугольной изометрией и диметрией, косоугольной фронтальной и горизонтальной изометрией и фронтальной косоугольной диметрией.