Рис. 13.6
Решение.
1. Задают оси аксонометрических проекций. На рис.13.6.б – оси прямоугольной изометрии, на рис.13.6.в – оси прямоугольной диметрии.
2. От точки О¢ на оси Х¢ откладывают координату ХА, взятую с ортогонального чертежа, - получают точку Ах¢. О¢Ах¢= О Ах = ХА .
3. Через А1¢ проводят прямую, параллельную оси У¢ и откладывают на ней координату УА, взятую также с ортогонального чертежа. При этом должен быть обязательно учтен коэффициент искажения по оси У.
Так, на рис.13.6.б в прямоугольной изометрии по направлению У¢ отложен отрезок, равный УА, а на рис.13.6.в в прямоугольной диметрии отложен отрезок 0,5УА (приведенный коэффициент искажения в прямоугольной диметрии по оси у равен 0,5).
А1¢ -вторичная проекции точки А.
4. Через А1¢ проведена прямая, параллельная оси Z, и на ней отложен отрезок, равный отрезку ZA. А1¢ А¢ = Ах А2 = ZA.
Итак, любую аксометрическую проекцию точки можно получить, построив в аксонометрии координатную ломаную линию, определяющую положение этой точки в пространстве.
Пример. Построить прямоугольную изометрическую проекцию шестиугольника по его ортогональному чертежу (рис. 13.7 а). 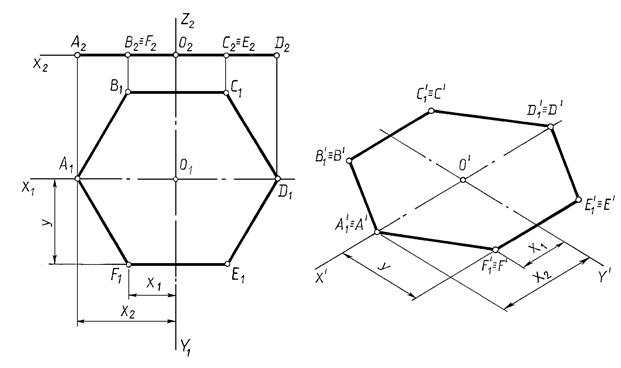
Рис. 13.7
Решение.
1. За оси координат X и Y принимаем оси симметрии шестиугольника.
2. Строим оси прямоугольной изометрии.
3. Плоский шестиугольник расположен в плоскости XОY, поэтому аксонометрия его совпадает со вторичной проекцией. Аксонометрию многоугольника строим по координатам вершин, пользуясь приведенными коэффициентами искажения, равными 1. Выполненные построения ясны из чертежа.
 2014-01-25
2014-01-25 997
997








