Средние величины
Средняя величина является обобщающей характеристикой совокупности однотипных явлений по изучаемому признаку. Средняя величина должна вычисляться с учетом экономического содержания определяемого показателя.
Все виды средних делятся на:
· степенные (аналитические, порядковые) средние (арифметическая, гармоническая, геометрическая, квадратическая);
· структурные (позиционные) средние (мода и медиана) – применяются для изучения структуры рядов распределения.
Средняя степенная (при различной величине k) определяется:
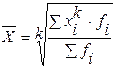 (1.1).
(1.1).
Таблица 1.1 - Виды средних степенных величин
| k | Наименование средней | Формула средней | Когда используется |
| Средняя арифметическая простая (невзвешенная) | 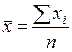 (1.2)
где xi – i-й вариант осредняемого признака ( (1.2)
где xi – i-й вариант осредняемого признака (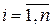 ); n – число вариант ); n – число вариант
| Используется, когда расчет осуществляется по несгруппированным данным | |
| Средняя арифметическая взвешенная | 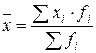 (1.3),
где fi – частота повторяемости i-го варианта (1.3),
где fi – частота повторяемости i-го варианта
| Используется, когда данные представлены в виде рядов распределения или группировок | |
| -1 | Средняя гармоническая взвешенная | 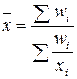 (1.4), где (1.4), где 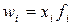 . .
| Используется, когда известны индивидуальные значения признака и веса W за ряд временных интервалов |
| -1 | Средняя гармоническая невзвешенная | 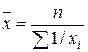 (1.5) (1.5)
| Используется в случае, когда веса равны |
| Средняя геометрическая невзвешенная | 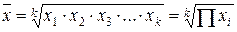 (1.6) (1.6)
| Используется в анализе динамики для определения среднего темпа роста | |
| Средняя геометрическая взвешенная | 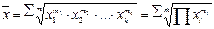 (1.7) (1.7)
| ||
| Средняя квадратическая невзвешенная | 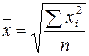 (1.8) (1.8)
| Используется при расчете показателей вариации | |
| Средняя квадратическая взвешенная | 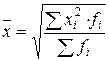 (1.9) (1.9)
|
В статистическом анализе также применяются степенные средние 3-го и более высоких порядков.
Правило мажорантности средних: с ростом показателя степени значения средних возрастают.
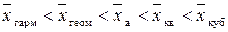 (1.10)
(1.10)
Средняя прогрессивная – средняя для “лучших” значений признака.
 2014-01-25
2014-01-25 770
770







