Показатели вариации признака. Вычисление средней арифметической взвешенной методом условных моментов

В каждом явлении и его развитии имеет место сочетание случайности и необходимости. При исчислении средних в силу действия закона больших чисел случайности взаимопогашаются, уравновешиваются и выявляются наиболее типичный уровень признака. Все явления статистической совокупности однокачественны – обладают единой материальной сущностью. В результате явления имеют определенную тенденцию к сходству, которая при расчете средних доводится до логического конца, до отыскания такого уровня признака, который имел бы место при полной тождественности единиц совокупности. Вычисление средней не является простой счетной операцией. Для научно обоснованного использования средних необходимо соблюдать следующие условия:

1. Средние величины должны рассчитываться только по качественно однородным совокупностям. Только при выполнении этого условия средняя как обобщающая характеристика отражает общее, типичное, закономерное, присущее всем единицам исследуемой совокупности. Средние, полученные для неоднородных совокупностей будут описательными, будут искажать характер изучаемого явления. В таких случаях метод средних используется в сочетании с методом группировок, позволяющим выделить однородные группы, по которым и исчисляются типические групповые средние.

2. Средняя должна исчисляться по совокупности, состоящей из достаточно большого числа единиц. Только в этом случае обеспечивается взаимопогашение случайных индивидуальных особенностей, что способствует проявлению основного, существенного, типичного, присущего всей массе единиц.

3. Каждая средняя характеризует изучаемую совокупность лишь по какому-либо одному признаку. Для того, чтобы дать всестороннюю характеристику совокупности, чтобы понять сущность средней, необходимо использовать систему взаимосвязанных средних величин.

4. Средняя должна вычисляться исходя:

а) из социально-экономического смысла признака, подлежащего осреднению; с тем, что по существу представляет собой данный признак, соотношениям и каких величин он определяется (логическая форма средней);

б) из характера исходных статистических данных, по которым определяется средняя.

Формула средней выводится для каждого конкретного случая и форма средней не может быть произвольной. В зависимости от характера исходных данных может быть несколько различных случаев решения, но в любом случае сохранится одна и та же логическая форма этой средней величины.

В каждом конкретном случае для реализации логической формы средней требуется одна из форм средней величины:

1) средняя арифметическая;

2) средняя гармоническая;

3) средняя геометрическая;

4) средняя квадратическая.

Итак, при выборе вида средней величины обычно исходят из логической сущности осредняемого признака и его взаимосвязи с итоговым показателем. Общий вид степенной средней имеет вид:

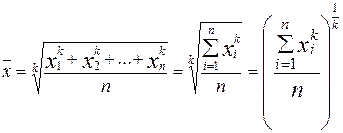
Если отдельные значения признака встречаются несколько раз, тогда частота повторения индивидуальных значений признака (вес) присутствует в расчетных формулах степенных средних. В этом случае общий вид степенной средней имеет вид:

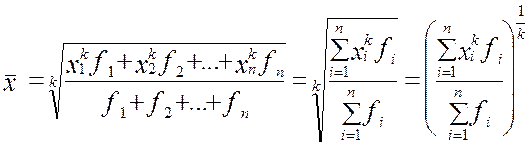
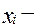варианты значений признака, индивидуальные значения осредняемого признака;

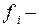частота повторения данного варианта, признак вес.

Запишем формулы различных видов степенных средних, придавая k значения: -1,0,1,2,.

При k = -1 получим среднюю гармоническую величину:

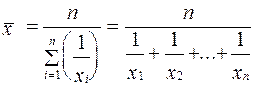(средняя гармоническая простая)

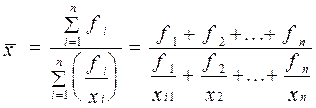(средняя гармоническая взвешенная)

При k = 0 получим среднюю геометрическую величину:

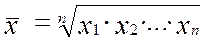(средняя геометрическая простая)

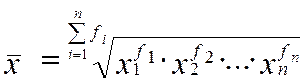(средняя геометрическая взвешенная)

(При этом степень корня совпадает с суммарной степенью отдельных значений признака).

При k=1 получим среднюю арифметическую:

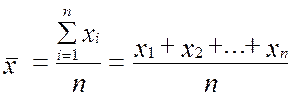(средняя арифметическая простая)

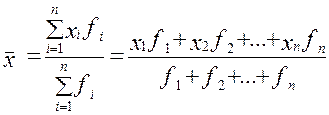(средняя арифметическая взвешенная)

При k=2 получим среднюю квадратическую величину:

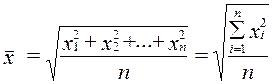(средняя квадратическая простая)

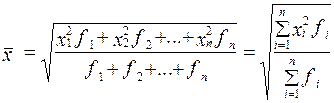(средняя квадратическая взвешенная).

Степенные средние разных видов, исчисленные по одной и той же совокупности, имеют различные количественные значения. Чем больше показатель степени k, тем больше величина соответствующей средней.

Рассмотрим применение различных видов средних величин на примере.