2014-01-25
726
Имеются следующие данные о стоимости и использовании фондов на предприятиях отрасли за 2 смежных квартала:
| Пред-приятие | 1 квартал | 2 квартал | ||
| Объем основных производственных фондов, млн. руб. | Фондоотдача, руб. | Объем произведенной продукции, млн. руб. | Фондоотдача, руб. | |
| 17,0 | 0,97 | 16,5 | 1,15 | |
| 9,2 | 1,20 | 11,1 | 1,25 | |
| 12,8 | 0,85 | 15,0 | 0,90 |
Определить средний уровень фондоотдачи в 1 и отдельно 2 кварталах. Формулу записать, используя буквенные обозначения. Указать вид средней величины.
Решение:
1 квартал.
а) логическая формула средней.
В соответствии с экономическим содержанием:
| Фондоотдача = | Объем производственной продукции ОПФ |
| Основные производственные фонды (ОПФ) |
б) по условию задачи в 1 квартале у нас известна фондоотдача и объем основных производственных фондов, отсюда определим объем произведенной продукции, т.е. соотношение будет иметь вид:
| Фондоотдача = | Фондоотдача  Объем ОПФ
|
| ОПФ |
г) обобщим данные по совокупности заводов и запишем формулу используя буквенные обозначения:
|
|
|
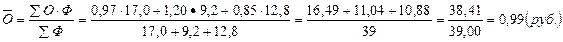
О – осредняемый признак; Ф – признак вес.
Средняя арифметическая взвешенная.
2 квартал.
Логическая формула средней фондоотдачи та же самая, т.е.
| Фондоотдача = | Объем продукции |
| Стоимости ОПФ |
Однако во 2 квартале нам известна фондоотдача и объем произведенной продукции, отсюда определим стоимости основных производственных фондов и соотношение будет иметь вид:
| Фондоотдача = | Объем производственной продукции |
| Объем произведенной продукции | |
| Фондоотдача |
Среднюю фондоотдачу необходимо рассчитывать в этом случае по следующему алгоритму:
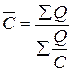- средняя гармоническая взвешенная.
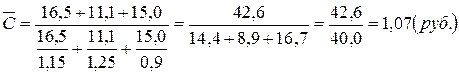
Вывод: Логическая формула средней одного и того же показателя (соотношением каких величин определяется этот показатель) всегда одна и та же. Однако, в зависимости от исходных данных применяются различные формы средних величин.
