По способу организации различают следующие виды выборки: собственно случайную или простую, расслоенную (типическую или районированную), серийную, механическую, комбинированную, ступенчатую и многофазную. По степени охвата единиц исследуемой совокупности различают большие и малые выборки.
В дальнейшем будем применять следующие условные обозначения:
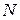 - объем генеральной совокупности (число входящих в нее единиц);
- объем генеральной совокупности (число входящих в нее единиц);
n - объем выборки (число обследованных единиц);
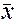 - генеральная средняя (среднее значение признака в генеральной совокупности);
- генеральная средняя (среднее значение признака в генеральной совокупности);
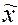 - выборочная средняя;
- выборочная средняя;
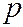 - генеральная доля (доля единиц, обладающих данным значением признака, в общем числе единиц генеральной совокупности), например, доля числа бракованных единиц в общем количестве единиц в данной партии изделий;
- генеральная доля (доля единиц, обладающих данным значением признака, в общем числе единиц генеральной совокупности), например, доля числа бракованных единиц в общем количестве единиц в данной партии изделий;
w - выборочная доля;
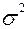 - генеральная дисперсия (дисперсия признака в генеральной совокупности);
- генеральная дисперсия (дисперсия признака в генеральной совокупности);
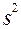 - выборочная дисперсия того же признака;
- выборочная дисперсия того же признака;
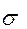 - среднее квадратическое отклонение в генеральной совокупности;
- среднее квадратическое отклонение в генеральной совокупности;
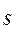 - среднее квадратическое отклонение в выборке.
- среднее квадратическое отклонение в выборке.
|
|
|
Простая случайная выборка
При простой случайной выборке отбор производится из всей массы единиц генеральной совокупности без предварительного расчленения ее на какие-либо группы, и единица отбора совпадает с единицей наблюдения.
В зависимости от способа отбора единиц различают:
1) отбор по схеме возвращенного шара, обычно называемый повторной выборкой. При повторном отборе вероятность попадания каждой отдельной единицы в выборку остается постоянной, так как после отбора какой-то единицы, она снова возвращается в совокупность и снова может быть выбранной;
2) отбор по схеме невозвращенного шара, называемый бесповторной выборкой. В этом случае каждая отобранная единица не возвращается обратно и вероятность попадания отдельных единиц в выборку все время изменяется (для оставшихся единиц она возрастает).
Согласно центральной предельной теореме А.М. Ляпунова при достаточно большом числе независимых наблюдений в генеральной совокупности с конечной средней и ограниченной дисперсией, вероятность того, что расхождение между выборочной и генеральной средней 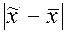 не превзойдет по абсолютной величине некоторую величину
не превзойдет по абсолютной величине некоторую величину 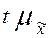 равна интегралу Лапласа:
равна интегралу Лапласа:
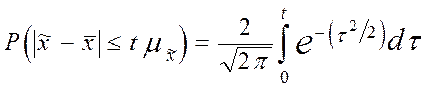
Величина 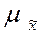 есть средняя квадратическая стандартная ошибка выборки (средняя возможная ошибка). Следовательно, что при достаточно большом числе независимых наблюдений, распределение выборочных средних, а следовательно, и их отклонений от генеральной средней, приближенно подчиняется нормальному распределению.
есть средняя квадратическая стандартная ошибка выборки (средняя возможная ошибка). Следовательно, что при достаточно большом числе независимых наблюдений, распределение выборочных средних, а следовательно, и их отклонений от генеральной средней, приближенно подчиняется нормальному распределению.
В математической статистике доказывается, что величина средней квадратической стандартной ошибки простой случайной повторной выборки может быть определена по формуле:
|
|
|
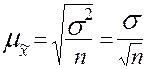 .
.
Следовательно, чем больше вариация признака, тем больше ошибка выборки и чем больше обследуется единиц, тем меньше будет величина расхождений выборочных и генеральных характеристик.
Величину 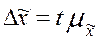 называют предельной ошибкой выборки. Она равна
называют предельной ошибкой выборки. Она равна 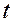 -кратному числу средних ошибок выборки. Допустим, что
-кратному числу средних ошибок выборки. Допустим, что 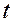 = 2. Тогда,
= 2. Тогда, 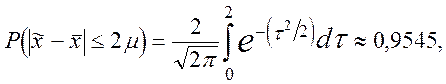 т.е. с вероятностью, равной 0,9545, можно ожидать, что ошибка выборочной средней не превысит удвоенной средней квадратической ошибки выборки. Таким образом, величина предельной ошибки выборки может быть установлена с определенной вероятностью.
т.е. с вероятностью, равной 0,9545, можно ожидать, что ошибка выборочной средней не превысит удвоенной средней квадратической ошибки выборки. Таким образом, величина предельной ошибки выборки может быть установлена с определенной вероятностью.
Приведем наиболее часто употребляемые уровни доверительной вероятности и соответствующие значения для выборок достаточно большого объема 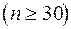 .
.
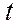
| 1,00 | 1,96 | 2,00 | 2,58 | 3,00 |
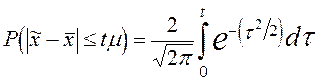
| 0,683 | 0,950 | 0,954 | 0,990 | 0,997 |
В формулу средней ошибки выборки входит дисперсия признака в генеральной совокупности, величина которой неизвестна. Для ее оценки приходится использовать выборочную дисперсию. Генеральная дисперсия 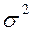 и выборочная дисперсия
и выборочная дисперсия 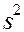 связаны соотношением
связаны соотношением 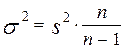 . Следовательно,
. Следовательно,
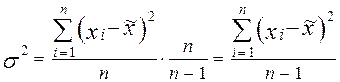 .
.
При достаточно большом объеме выборки 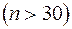 полагают, что
полагают, что
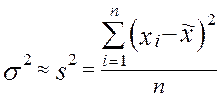 ,
,
или для сгруппированных данных:
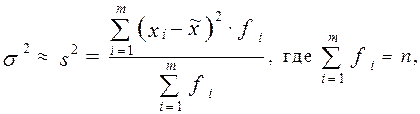
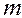 - число групп на которые разбита выборочная совокупность.
- число групп на которые разбита выборочная совокупность.
Средняя квадратическая ошибка случайной бесповторной выборки определяется по формуле
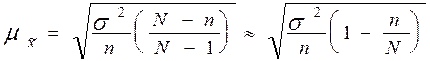 .
.
Выборочное наблюдение проводится в целях распространения выводов, полученных по данным выборки, на генеральную совокупность. Одной из основных задач является оценка по данным выборки интересующих нас характеристик (параметров) генеральной совокупности.
Выборочное наблюдение дает возможность определить среднюю арифметическую выборочной совокупности 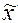 и величину предельной ошибки этой средней
и величину предельной ошибки этой средней 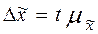 , которая показывает (с определенной вероятностью), насколько выборочная средняя может отличаться от генеральной средней в большую или меньшую сторону. Тогда величина генеральной средней будет представлена интервальной оценкой, для которой нижняя граница будет равна
, которая показывает (с определенной вероятностью), насколько выборочная средняя может отличаться от генеральной средней в большую или меньшую сторону. Тогда величина генеральной средней будет представлена интервальной оценкой, для которой нижняя граница будет равна 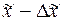 , а верхняя граница
, а верхняя граница 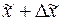 . Пределы, в которых с данной степенью вероятности будет заключена неизвестная величина оцениваемого параметра, называют доверительными, а вероятность Р - доверительной вероятностью.
. Пределы, в которых с данной степенью вероятности будет заключена неизвестная величина оцениваемого параметра, называют доверительными, а вероятность Р - доверительной вероятностью.
Доверительный интервал для генеральной средней можно записать как:
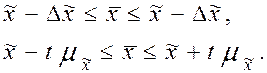
 2014-01-25
2014-01-25 833
833








