Гиперболоид вращения – поверхность, образованная вращением прямой вокруг скрещивающейся с ней оси.
Линейчатая поверхность, которую необходимо построить, называется однополосным гиперболоидом вращения. Она образуется вращением прямой l вокруг скрещивающейся с ней оси i. Ближайшая к оси вращения точка образующей описывает наименьшую параллель – горло гиперболоида. Главный меридиан – гипербола.
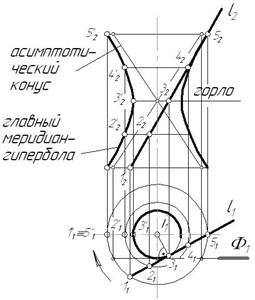
Рис. 6.7
Эта поверхность может быть также получена вращением очерковой гиперболы вокруг своей мнимой оси i. Поверхность имеет два семейства прямолинейных образующих, т.к. через одну точку можно провести две прямые – восходящую прямую (как в данной задаче) и нисходящую прямую. Это видно, если касательно к горлу гиперболоида провести плоскость 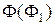 , параллельную оси вращения. Такая плоскость пересекает поверхность по двум прямым. Вторая восходящая прямая образует второе семейство образующих.
, параллельную оси вращения. Такая плоскость пересекает поверхность по двум прямым. Вторая восходящая прямая образует второе семейство образующих.
Если в центре горла гиперболоида построить конус с таким же углом наклона образующих, как у гиперболоида, то получим так называемый асимптотический конус, к которому поверхность приближается в бесконечности.
 2014-01-25
2014-01-25 874
874








