Для нахождения области сходимости функционального ряда удобно пользоваться признаками Даламбера или Коши. Но члены функционального ряда при различных х могут быть как положительными, так и отрицательными, поэтому члены данного ряда берут по абсолютной величине. Например, в признаке Даламбера вычисляют предел 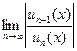 < 1.
< 1.
При этом концы интервалов исследуются отдельно, т.к. на концах указанные пределы равны 1, и признаки ответа не дают.
Пример 1. Найти область сходимости функционального ряда 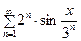 .
.
Решение. Если х = 0, то 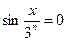 , и ряд состоит из нулей, т.е. сходится. Применим признак Даламбера для х ≠ 0:
, и ряд состоит из нулей, т.е. сходится. Применим признак Даламбера для х ≠ 0:
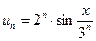 ,
, 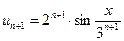 ,
, 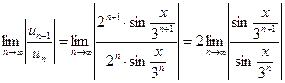 .
.
Так как 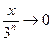 и
и 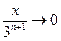 при
при 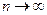 , то
, то 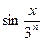 ~
~ 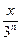 ,
,
а 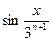 ~
~ 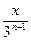 и
и
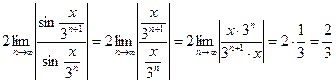 < 1.
< 1.
По признаку Даламбера ряд сходится. Значит, ряд сходится при любом х, т.е. область сходимости ряда – вся числовая ось.
Пример 2. Найти область сходимости функционального ряда 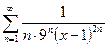 .
.
Решение. Заметим, что, так как члены данного функционального ряда положительны, то вычислять предел можно без знаков модуля:
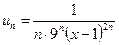 ,
, 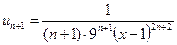 ,
,
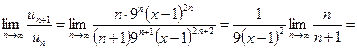
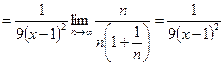 .
.
По признаку Даламбера ряд сходится, если  < < 1, откуда
< < 1, откуда 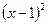 >
> 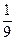 ,
, 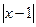 >
> 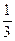 , что равносильно двум неравенствам
, что равносильно двум неравенствам 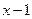 >
> 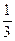 и
и 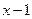 < –
< –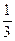 или
или 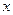 >
>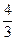 и
и 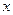 <
< 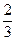 . Следовательно, получены два промежутка
. Следовательно, получены два промежутка 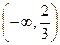 ,
, 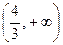 , где сходится ряд.
, где сходится ряд.
|
|
|
Концы промежутков 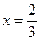 и
и 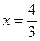 остались неисследованными, так как в случае, если
остались неисследованными, так как в случае, если 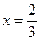 или
или 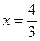 , выражение
, выражение  = 1, и признак Даламбера ответа не даёт. Поэтому концы интервала исследуем отдельно.
= 1, и признак Даламбера ответа не даёт. Поэтому концы интервала исследуем отдельно.
Подставив в данный ряд 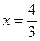 , получим ряд
, получим ряд
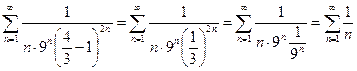 ,
,
который расходится как гармонический.
Подставив в данный ряд 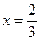 , получим опять гармонический ряд
, получим опять гармонический ряд
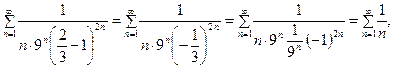
который тоже расходится.
Поэтому областью сходимости данного ряда являются два интеграла: 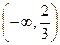 ,
, 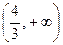 .
.
 2014-01-25
2014-01-25 684
684








