Введем на множестве комплексных чисел отношение равенства двух чисел, а также операции сложения, вычитания, умножения и деления.
· Два комплексных числа 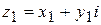 и
и 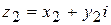 называются равными, если равны их действительные и мнимые части:
называются равными, если равны их действительные и мнимые части:
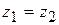
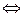
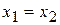 ,
, 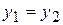
В частности, 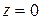
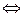
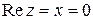 ,
, 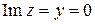 .
.
Заметим, что:
1) одно равенство 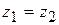 комплексных чисел равносильно двум равенствам
комплексных чисел равносильно двум равенствам 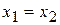 и
и 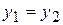 действительных чисел;
действительных чисел;
2) понятия «больше», «меньше» для комплексных чисел не определяются.
· Суммой (разностью) комплексных чисел 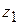 и
и 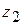 называется комплексное число
называется комплексное число
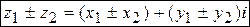 .
.
Пример. Найти сумму комплексных чисел 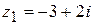 и
и 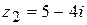 .
.
Решение. 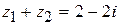 .
.
Операция сложения комплексных чисел обладает свойствами:
1. 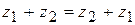 (переместительный закон)
(переместительный закон)
2. 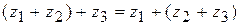 (сочетательный закон)
(сочетательный закон)
3. 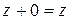
4. Для каждого комплексного числа 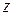 существует такое число
существует такое число 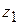 , которое в сумме дает нуль:
, которое в сумме дает нуль: 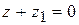 . Оно называется противоположнымкомплексным числом для
. Оно называется противоположнымкомплексным числом для 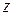 и обозначается
и обозначается 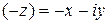 . Таким образом,
. Таким образом, 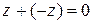 .
.
· Произведением комплексных чисел 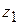 и
и 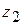 называется комплексное число
называется комплексное число
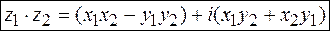 .
.
Отсюда получаем важное соотношение:
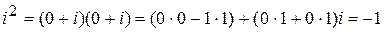 , то есть
, то есть 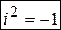 .
.
Не стоит запоминать формулу умножения – правило умножения получается формально путем умножения двучленов 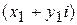 и
и 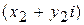 с учетом
с учетом 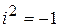 .
.
Пример. Найти произведение комплексных чисел 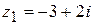 и
и 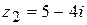 .
.
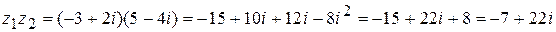 .
.
Операция умножения комплексных чисел обладает свойствами:
1. 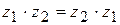 (переместительный закон)
(переместительный закон)
2. 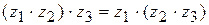 (сочетательный закон)
(сочетательный закон)
3. 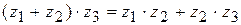 (распределительный закон)
(распределительный закон)
4. Произведение взаимно сопряженных комплексных чисел 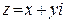 и
и 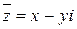 равно квадрату их модуля:
равно квадрату их модуля: 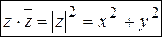 .
.
· Частным от деления комплексного числа 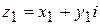 на комплексное число
на комплексное число 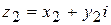 (
(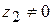 ) называется комплексное число, равное
) называется комплексное число, равное
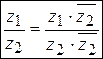 .
.
Найдем действительную и мнимую части частного двух комплексных чисел. Домножим числитель и знаменатель на число 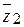 , сопряженное знаменателю:
, сопряженное знаменателю:
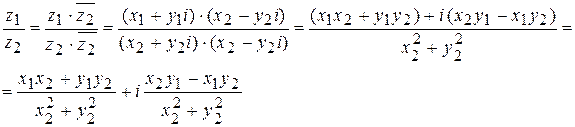
Сама формула громоздка и трудно запоминается. Поэтому проще умножить числитель и знаменатель дроби 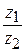 на
на 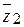 , то есть на число, сопряженное знаменателю, и произвести преобразования.
, то есть на число, сопряженное знаменателю, и произвести преобразования.
Пример. Найти частное от деления комплексного числа 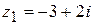 на число
на число 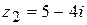 .
.
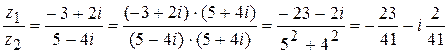 .
.
 2014-01-25
2014-01-25 732
732








