Формула Тейлора

Способ Маклорена был красив и прост, но в более общем виде задача разложения функции в степенной ряд была решена Тейлором. Постановка задачи была следующей. Приблизить f (x) в окрестности точки х = х ₀ многочленом п – й степени 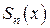так, чтобы сам многочлен в точке х ₀ совпадал с заданной функцией f (x), и значения всех его производных до п – го порядка в точке х ₀ совпадали со значениями соответствующих производных f (x).В итоге решением задачи стала формула Тейлора (7).

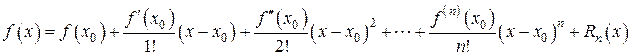, (7)

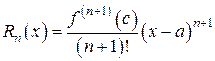где – (8)

остаточный член формулы Тейлора, а точка с – некоторая промежуточная точка между точками а и х.

Если f (x) имеет производные любых порядков (т.е. бесконечно дифференцируема) в окрестности точки х = х ₀ и остаточный член 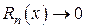при 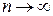(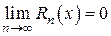), то из формулы (7) получается разложение функции f (x) по степеням (х – х ₀), называемое рядом Тейлора:

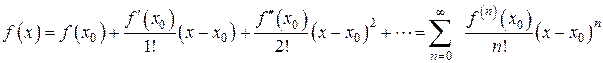(9)

При х ₀ = 0 ряд Тейлора превращается в ряд Маклорена:

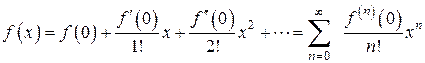(10)

Таким образом, результат Маклорена оказался лишь частным случаем исследований Тейлора, и поэтому разложения функций в степенные ряды получили в математике название «ряды Тейлора».

Отметим, что ряд Тейлора – Маклорена можно формально построить для любой бесконечно дифференцируемой функции (это необходимое условие) в окрестности точки х ₀. Но отсюда еще не следует, что он будет сходиться к данной функции, он может расходиться или сходиться к посторонней функции.

Т е о р е м а 1. Для того чтобы ряд Тейлора (9) функции f (x) сходился к f (x) в точке х, необходимо и достаточно, чтобы в этой точке остаточный член формулы Тейлора (7) стремился к нулю при 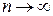, т. е. чтобы .

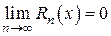Т е о р е м а 2. Если модули всех производных 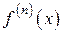функции f (x) ограничены в окрестности точки 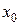одним и тем же числом М > 0, то для любого х из этой окрестности ряд Тейлора сходится к функции f (x), т. е. имеет место разложение (9).

З а м е ч а н и е. Гарантией сходимости ряда Тейлора функции f (x) к ней самой является элементарность функции f (x).

Так как исследователь в большинстве случаев имеет дело с элементарными функциями, то сходимость ряда Тейлора к f (x) обычно гарантирована. Для неэлементарных функций можно воспользоваться условием ограниченности их производных.

Примером Коши называют неэлементарную функцию вида:

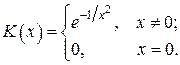(11)

Показано, что К (х) имеет в точке 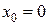производные всех порядков, причем 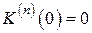при всяком п. Ряд Маклорена функции К (х) имеет вид:

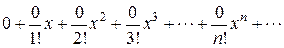(12)

Он сходится, но его сумма S (x) в любой точке х равна нулю, а не К (х). Таким образом, ряд Маклорена, порожденный функцией К (х), сходится к посторонней функции 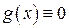, а не к К (х).