2014-01-25
747
Перпендикулярность прямой и плоскости. Теорема о свойстве прямого угла. Позиционные задачи
Лекция №4
Контрольные вопросы
1. Сформулируйте условия принадлежности точки плоскости и прямой плоскости.
2. Как построить прямую параллельную заданной плоскости?
3. Какие точки называются конкурирующими?
4. Как провести в плоскости горизонталь и фронталь?
5. Сформулируйте условие параллельности плоскостей.
6. Сколько можно провести плоскостей параллельных данной через какую-либо точку пространства?
7. Как решается задача на построение линии пересечения плоскостей?
Построение взаимно перпендикулярных прямых и плоскостей является важной графической операцией при решении метрических задач.
Построение перпендикуляра к прямой или плоскости основывается на свойстве прямого угла, которое формулируется следующим образом: если одна из сторон прямого угла параллельна плоскости проекций, а другая не перпендикулярна ей, то угол проецируется в натуральную величину на эту плоскость.
 |
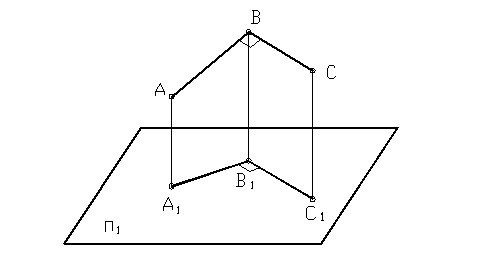Рисунок 28
Сторона ВС прямого угла АВС, изображенного на рисунке 28, параллельна плоскости П1. Следовательно, проекция угла АВС на эту плоскость будет представлять прямой угол А1В1С1=90.
