Прежде чем приступить к решению задачи необходимо выяснить, какой признак является результативным, а какой − факторным. В рассматриваемом примере результативным признаком является «Тарифный разряд», а факторным признаком − «Номер (название) предприятия».
Тогда имеем три группы (предприятия), для которых необходимо рассчитать групповую среднюю 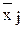 и внутригрупповые дисперсии
и внутригрупповые дисперсии 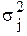 :
:
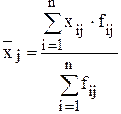
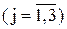 ,
, 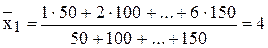 ,
,
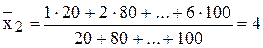 ,
,
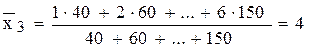 ,
,
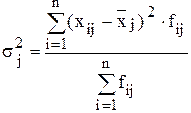
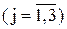 ,
,
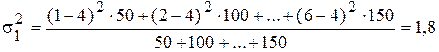 ,
,
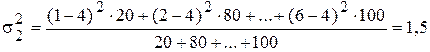 ,
,
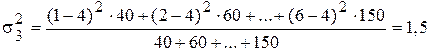 .
.
Результаты расчета сведем в таблицу:
| Предприятие | Групповая средняя,
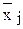
| Внутригрупповая дисперсия,
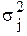
|
| 1,8 1,5 1,5 |
Средняя из внутригрупповых дисперсий рассчитаем по формуле:
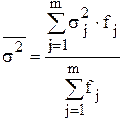
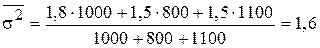 .
.
Межгрупповую дисперсию определим как:
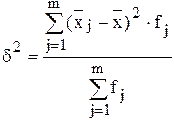 , где
, где 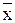 можно рассчитать:
можно рассчитать:
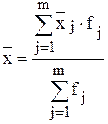 ,
, 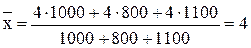
либо: 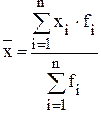 ,
, 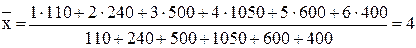 ,
,
тогда: 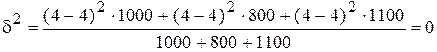 .
.
Общая дисперсия будет равна: 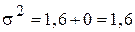 .
.
Общую дисперсию также можно рассчитать и по одной из следующих двух формул:
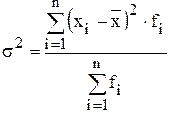
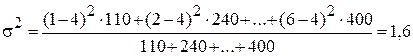
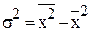
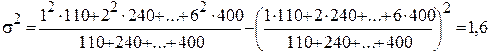 .
.
При решении практических задач часто приходится иметь дело с признаком, принимающим только два альтернативных значения. В этом случае говорят не о весе того или иного значения признака, а о его доле в совокупности. Если долю единиц совокупности, обладающих изучаемым признаком, обозначить через «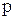 », а не обладающих − через «
», а не обладающих − через «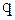 », то дисперсию можно рассчитать по формуле:
», то дисперсию можно рассчитать по формуле:
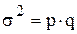 .
.
 2014-01-25
2014-01-25 754
754








