П.Машина Тьюринга – постановка задачи

Машина с бесконечной памятью

Вначале остановимся на модели Тьюринга [ ]Интеллектуальной подоплекой, стимулировавшей появление работы Тьюринга являются,по-видимому, проблема поиска алгоритма - эффективной процедуры решения математической задачи. Можно ли описать все в принципе описываемые процессы, решить все математические задачи? И Тьюринг дает несколько неожиданный ответ на этот вопрос: да, эта процедура может быть выполнена с помощью некоторой очень простой машины. Простота машины гарантирует отсутствие у нее «инициативности» или «разумности» и тогда описание является полным и процедура является «эффективной». Следуя Тьюрингу можно сделать радикальное предположение, что любая процедура, которую было бы «естественно» назвать эффективной, фактически может быть реализована с помощью машины. Здесь уместно подчеркнуть, что рассматриваемые вопросы носят субъективный характер и при их обсуждении можно лишь убеждать, приводя некоторые доводы.. Здесь ничего нельзя доказать, однако, как бы то ни было, эта теория дает впечатляющие результаты. Например, попытка дать определение «эффективной» процедуры наталкивается на различные трудности- слишком уж сложным. является это интуитивное понятие. Можно, следуя Минскому М., дать следующее определение: эффективная процедура есть множество сообщаемых нам время от времени правил, точно регламентирующих наше поведение. Чтобы понимание правил было единообразным и не допускало «смыслового люфта», то наряду с формулировками правил, уместно задать конструкцию устройства, интерпретирующего эти правила. Чтобы не создавать эту конструкцию заново для каждого последующего вычисления, желательно иметь некоторое единообразное семейство устройств, выполняющих предписания. При этом наиболее подходящей формулировкой может служить следующая, в которой мы устанавливаем:1) язык, на котом описывается множество правил поведения. и2) одну-единственную машину, которая может интерпретировать утверждения, сделанные на этом языке и, таким образом, выполнять шаг за шагом каждый точно определенный процесс.Трудно ожидать, что найдется одно-единственное устройство, способное интерпретировать и выполнять все правила, встречающиеся во всех эффективных процедурах. Казалось бы, что необходим целый ряд все более сложных машин решающих все более и более сложные задачи.Однако, как это ни покажется невероятным, но здесь нет проблем! Можно построить одну машину, конструкция которой удивительно проста и не зависит от сложности решаемой задачи. Иначе говоря, оказывается возможным предложить язык для описания правил и простую «универсальную» интерпретирующую машину, которая может иметь дело со всеми эффективными процедурами. Основная идея состоит в замене качественного увеличения сложности машины простым количественным увеличением ее объема памяти. Тьюринг обнаружил, что подобные машины могут производить сложные вычисления. Им был сформулирован так называемый тезис Тьюринга: любой процесс, который было бы естественно назвать эффективной процедурой, может быть реализован машиной Тьюринга. Когда понимаешь, как на самом деле примитивны машины Тьюринга, то остается лишь удивляться смелости тезиса. Однако, практика нескольких десятилетий, прошедших после появления этой работы, подтверждает справедливость точки зрения Тьюринга Для любой процедуры, которую математики соглашались назвать «эффективной», тем или иным способом была показана ее эквивалентность процедуре, реализуемой машиной Тьюринга. Рассмотрим подробно устройство и работу машины Тьюринга. Машина Тьюринга (МТ) представляет собой автомат с конечным числом состояний, соединенный с внешней памятью, которая конструктивно выполнена в виде бесконечной ленты. Последняя разбита на деления – ячейки. Автомат связан с лентой посредством головки, которая несет три функции: может считывать содержимое ячейки и записывать в ячейку некоторый символ. Кроме того, головка может сдвигаться влево, вправо или оставаться на месте в процессе выполнения очередного шага вычислений.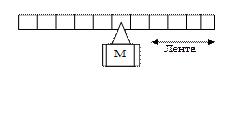 напомним, что машина с конечным числом состояний характеризуется алфавитом 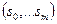входных символов, алфавитом 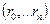выходных символов, множеством 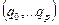внутренних состояний и парой функций, которые описывают связь между входом, внутренним состоянием и последующим поведением. Для того, чтобы в описании фигурировала внешняя лента это описание следует несколько изменить. Входные символы останутся прежними и будут в точности теми же, которые могут быть считаны с ленты по одному символу на ячейку. Входом машины М в момент времени t будет, как и прежде, как раз тот символ, который напечатан в ячейке, обозреваемой машиной в этом момент. Результирующее изменение состояния, как и прежде, определяется функцией G. Выход машины М выполняет теперь две функции: 1) запись символа в обозреваемую ячейку (возможна замена ранее записанного там символа) и 2) передвижение вдоль ленты в ту или другую сторону. Таким образом, выход R имеет две компоненты. Одна компонента ответа – это просто символ из того же самого множества 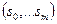который должен быть записан в обозреваемую ячейку; вторая компонента - один из двух символов «0» (означает «сдвинуться влево») или 1 (означает»сдвинуться вправо»), что оказывает соответствующее воздействие на положение машины. Итак, удобно предположить, что машина Тьюринга описывается тремя уравнениями. 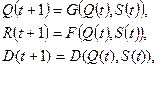где D(t) – новая функция, которая определяет, куда должна двигаться машина. В каждом такте работы машина начинает с некоторого состояния 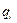, считывает символ 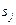, написанный в ячейке находящейся над головкой, печатает там новый символ 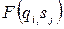, сдвигается влево или вправо в соответствии со значением 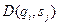и затем переходит в новое состояние 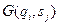. Когда символ печатается на ленте, предыдущий символ на этом месте стирается. Конечно, если стирания не требуется, то можно напечатать тот же символ, который считывался, в этом случае 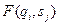принимает значение 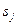. Так как машина может передвигаться вдоль ленты в любую сторону, то она может вернуться к напечатанному ранее месту, чтобы использовать записанную туда информацию. Это, как будет видно в дальнейшем, делает возможным использовать ленту для запоминания произвольно большого количества информации. Примеры - впереди!В предлагаемой модели считается, что лента бесконечна в обе стороны. Но мы наложим ограничение: в тот момент, когда машина запускается в работу, лента должна быть пустой, за исключением некоторого конечного числа ячеек. В связи с этим ограничением можно полагать, что на самом деле лента конечна в каждый момент времени, но всякий раз, когда мы подходим к ее концу, она автоматически наращивается еще на одну ячейку. Существует несколько способов описания МТ, но все они принципиально схожи и различие между ними в некоторых технических деталях (машина Поста, устройство, описанное Клини нами рассматриваться не будут). Для наших целей удобнее описывать МТ диаграммами состояний. Нам важно показать, что МТ с их неограниченной памятью могут производить вычисления, выходящие за пределы возможностей конечных машин – это легче показать на примерах, изложенных на языке диаграмм, чем на языке таблиц функций. Та часть машины, которая имеет конечное число состояний может быть описана следующей пятеркой: старое состояние, обозреваемый символ, новое состояние, записанный символ, направление движения, т.е.: 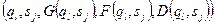или 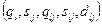,т.е. пятеркой, в которой третий, четвертый и пятый символы определяются по первому и второму с помощью трех упомянутых функций 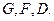Таким образом, для некоторой МТ можно было бы сопоставить следующее описание: 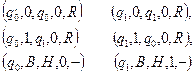или просто 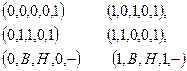где символ Н (от halt- «стоп») используется для обозначения заключительного состояния.(замечание: лента вместе с МТ представляет замкнутую систему) Рассмотрим несколько примеров вычислений с использованием МТ. Пример 1. Счетчик четности. Рассмотрим машину сигнал на выходе которой (в дальнейшем просто «выход») равен 1 или 0 в зависимости от того четное или нечетное число единиц записано в строке. Входная последовательность представлена записью на ленте МТ В конце указанной последовательности имеется дополнительный символ В. Машина запускается в работу (из состояния 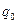) под первым символом последовательности. Символ В говорит, что последовательность закончена. Машине требуется два состояния – одно для нечетного числа единиц, а другое – для четного: состояния меняются всякий раз, когда встречается 1. Соответствующая конечная машина представлена в таблице ….. Работа машины происходит так: 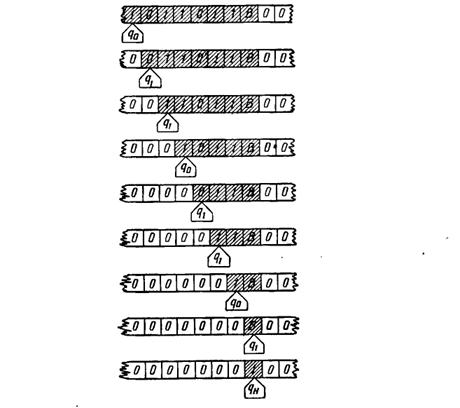Машина завершает работу против ячейки В. Входная последовательность символов оказывается стертой. Задача. Замените пятерки так, чтобы входная последовательность символов не стиралась. В рассмотренном примере машина сдвигается только вправо. В таком случае нет возможности записать информацию на ленте и возвратиться к ней позже. Следовательно, нельзя ожидать, что она делает что-либо, что не может быть сделано без каких-либо дополнительных устройств машиной с конечным числом состояний. Известно, что такого рода действия могут выполняться конечными машинами. Пример2 Преобразователь единичного кода в двоичный. Пусть последовательность задана в виде серии единиц на бесконечной ленте, пустой на отдельных позициях: 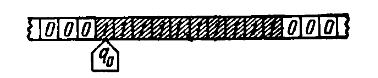Машина начинает свою работу с крайней летней единицы. Ее диаграмма показана на рис.. 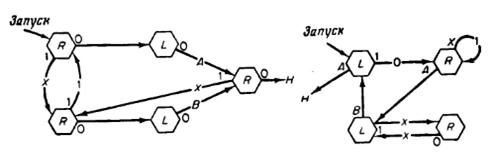Парные состояния, соответствующие движению в правую сторону, используются как в счетчике четности. При этом происходит вычеркивание единиц через одну (они заменяются символами Х). Когда строка исходных символов проверена на четность, машина переходит в одно из состояний, ассоциированных с движением в левую сторону, которое отмечается символами А или В, вносимыми в первую свободную ячейку слева. Когда все единицы в строке вычеркнуты, машина останавливается. Оказывается, что последовательность символов А и В является двоичной записью исходного единичного кода. Чтобы убедиться в этом достаточно установить, что в момент перехода в состояние R, ассоциированное с движением вправо, состояния ленты имеют вид, показанный ниже. 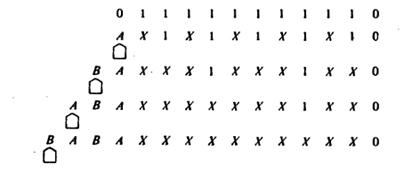Таким образом, ответ есть ВАВА=1010, что и есть запись 10 в двоичной системе счисления. Вычисления состоят в последовательном делении на 2, записи остатка (т.е. А или В), после чего процесс повторяется по отношению к частному, пока частное не станет равным нулю. Структура этого процесса несколько более сложная, чем в предыдущих примерах. Реализация проверки на четность, для которой требуется два состояния. Может быть истолкована, как подпроцесс, который повторяется снова и снова, пока не выполнится некоторое условие, обнаруживаемое «контролирующим» процессом. Мы имеем «цикл в цикле» и можем различить иерархию управления в ее простейшем виде. Этот тип вычислений не может быть выполнен машинами с конечным числом состояний. Задача. Оказывается, что точно такой же результат может быть достигнут двоичной пересчетной схемой, для которой требуются только два состояния и тот же самый алфавит! Можно ли предложить такую машину Тьюринга с двумя состояниями? Множительное устройство, работающее в единичном коде Рассматриваемая машина перемножает два числа m и n, заданных в единичном коде, т.е. представленных на ленте в виде серий единиц. В следующем виде: Машина начинает работу под символом В. Если, например участок ленты имеет вид: 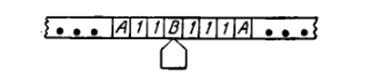то конечный результат имеет вид:

или 2х3=6, где ответ представлен серией символов Х справа от символа А. И в этом случае мы имеем дело с вычислениями, которые не могут быть выполнены машиной с конечным числом состояний.

Задача Предложите конструкцию МТ для 1) вычисления квадрата числа n, где n представляется в виде

1) Вычисления суммы двух двоичных чисел представимых в виде

Предполагается, что они имеют одинаковое количество цифр.

Здесь означает, что ячейка содержит 1 или 0.

2) Определения, является ли число простым (очень сложно!)

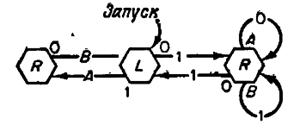
Упражнение. Опишите поведение машины, диаграмма переходов которой изображена на следующем рисунке. Предполагается, что машина начала работу на пустой ленте.

Задача. Постройте МТ для вычисления:

1) произведения двух двоичных чисел mи n;

2) степенной функции .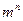

Рассмотренные примеры использования МТ имели своей целью показать, что эти устройства могут делать многое из того, что не могут делать машины с конечным числом состояний и что они могут делать необычайно сложные вещи, несмотря на сравнительно простые структуры. С другой стороны можно было наблюдать характерную для МТ неэффективность, связанную с многочисленными повторяющимися проходами головки вдоль длинных кусков ленты даже при выполнении самой элементарной операции перемещения временного маркера.

Никто всерьез и не предполагал использовать структуру, свойственную МТ для проведения практических вычислений. Однако, несмотря на малое быстродействие МТ далеко не всегда используют емкость ленточной памяти неэффективно. Например, можно построить машину, определяющую, является ли n-разрядное двоичное число простым, используя менее чем n дополнительных ячеек ленты. Следует также отметить, что высокое быстродействие обычных ЭВМ основано на произвольной выборке данных из памяти, которая только внешне позволяет обойти задачу последовательного поиска вдоль ленты. Можно представить МТ с трехмерной лентой и привести доводы в пользу того, что МТ такого типа в общем имеют не меньшее быстродействие, чем другие типы машин с конечным числом состояний и дополнительной памятью.

Оказывается, даже самые сложные из возможных вычислительных процедур, можно выполнить с помощью МТ, фиксированные структуры которых содержат всего лишь десятки элементов. Можно представить себе межзвездного робота, к надежности которого предъявляются очень высокие требования, но который выполняет вычисления очень медленно, потому что запас времени у него – сама вечность.

Существуют модификации МТ, например многоленточные МТ, которые по эффективности ближе к обычным вычислительным машинам. Рассматривать эти модели мы не будем.

Теорема Беннета в приложениях

Напомним формулировку :Теорема Беннета

Ч. Беннет в 1971 г. доказал возможность построения обратимой машины Тьюринга, т.е. такой, которая не теряет информации и, следовательно, в процессе работы может затрачивать любое заранее заданное малое количество энергии

можно доказать, что если имеется обычная машина Тьюринга, то можно построить обратимую трехленточную машину Тьюринга, которая не хуже обычной при любых стандартных входных данных и в конце вычислений даже превосходит ее, оставляя только эти входные данные и требуемые выходные. Обратимая машина производит вычисления в три стадии, при этом третья стадия служит для описания первой. Это утверждение носит название теоремы Ч.Беннета.