2014-01-25
1060
Флуктуация определяется дисперсией случайной величины
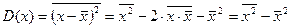. (152)
Здесь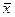 
- среднее значение случайной величины x, 
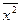- среднее значение ее квадрата. Флуктуацию удобнее определять среднеквадратичным значением
.
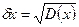Пусть Q – обобщенная координата (параметр) классической системы погруженной в термостат при температуре T и F – обобщенная сила соответствующая обобщенной координате. Покажем, что дисперсия (или флуктуация) величины Q определяется формулой
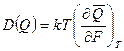. (153)
Можно показать, что вероятность термодинамической системы погруженной в термостат и «открытой» по параметру Q определяется формулой
.
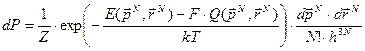Здесь мы выразили величину Q через обычные координаты и импульсы. Статистический интеграл системы
.
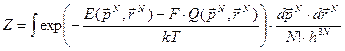Среднее значение Q
.
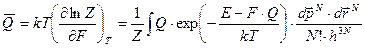Дифференцируем среднее значение
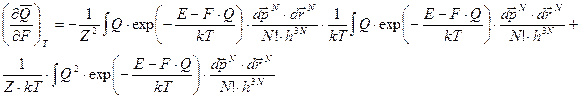
После преобразования
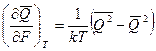. Что и требовалось доказать.
Применим формулу (153) для конкретных случаев.
d Задача. Определить флуктуации энергии системы в термостате при «замкнутых» остальных параметрах (объеме, числе частиц).
Формулу (153) можно представить в виде
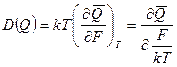. (153)
Тогда для энергии «обобщенной силой» формально является величина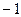 
. Используя (153), получаем
.
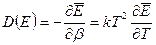Для идеального одноатомного газа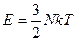 
, поэтому
.
.
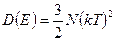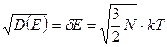Относительная величина флуктуации энергии
.
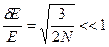d Задача. Определите флуктуацию объема системы погруженной в термостат и открытой по объему (фиксировано давление в системе, подвижный поршень).
В этом случае для объема сопряженной величиной (обобщенной силой) является (- p) «отрицательное» давление. В соответствии с общей формулой
.
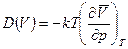Для идеального газа
.
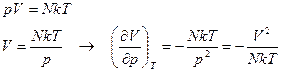
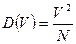Относительная среднеквадратичная флуктуация
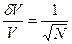
d Задача. Определите флуктуацию числа частиц в системе погруженной в термостат и открытой по числу частиц. Объем в системе фиксирован.
Для числа частиц обобщенной силой является химический потенциал, поэтому
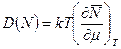. (154)
Для идеального газа
.
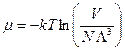Отсюда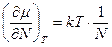 
. Значение производной подставляем в (154).
.
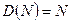Относительная среднеквадратичная флуктуация
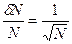. (155)
d Задача. Определите флуктуацию угла поворота зеркала гальванометра. Считайте исполнительный механизм гальванометра термодинамической системой погруженной в термостат открытой по углу поворота.
Для угла поворота зеркала обобщенной силой является момент упругих сил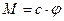 
. c – коэффициент упругости нити подвески зеркала. В соответствии с формулой (153)
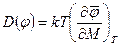
Так как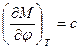 
, то
.
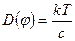Если гальванометр «не нагружен» током, то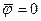 
и
; 
.
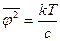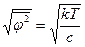Этот результат можно получить, используя теорему о равномерном распределении энергии по степеням свободы. Измерительная часть гальванометра является крутильным маятником, который имеет две термодинамические степени свободы (потенциальную и кинетическую).[40] Приравниваем среднюю потенциальную энергию маятника величине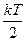 
и получаем тот же результат.
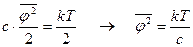. (156)
d Задача. Определите флуктуацию электрического заряда на обкладках конденсатора, которые замкнуты через сопротивление величиной R.
Обобщенной силой к величине заряда является напряжение, поэтому в соответствии с общей формулой (учитываем, что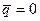 
)
.
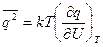Учитывая, что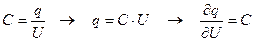 
, получаем
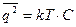. (157)
d Задача. Используя результат предыдущей задачи, определите время разрядки конденсатора заряженного до напряжения U. Схема конденсатора погружена в термостат с температурой T.
Разряд конденсатора определяется формулой
.
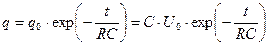Без учета дискретности заряда и термодинамики время разрядки конденсатора равно бесконечности. Учитывая термодинамику системы можно определить время разряда конденсатора по времени, при котором заряд конденсатора становится равным флуктуационному заряду, который определяется формулой (157). В соответствии с этим записываем
.
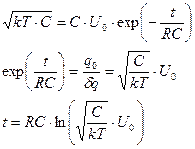Сделаем расчет для C = 1 мкФ, U0 = 10 В, R = 100 кОм. В этом случае RC = 0,1 сек. q0 = 10-5 Кл.
.
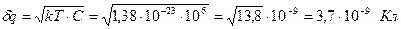
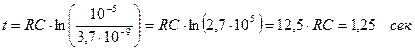IV. Компьютерные задачи по статистической термодинамике.
Задача 1. Преобразовать равномерное распределение псевдослучайных чисел генерируемых программой RND к распределению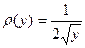 
. Эта функция плотности вероятности была получена в задаче «гравитационный кузнечик» (тело свободно падает в поле тяготения).
Задача 2. Преобразовать равномерное распределение псевдослучайных чисел генерируемых программой RND к линейной функции плотности вероятности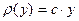 
(на интервале 0 – 1).
Задача 3. Провести компьютерное моделирование релаксации к равновесному распределению в неравновесном микроканоническом ансамбле (замкнутой системе). Неравновесное состояние представить линейным распределением вероятности состояний. Релаксацию проводить по максимуму энтропии.
Задача 4. Провести компьютерное моделирование методом Монте-Карло системы независимых спинов во внешнем поле (канонический ансамбль). Сравнить «экспериментальные» средние характеристики (энергия, флуктуация энергии) с теоретическими величинами.
Задача 5. Провести динамическое компьютерное моделирование системы «пружинный маятник + частица». Одномерная система. Маятник прикреплен к левой границе отрезка. Свободная частица «блуждает» в правой свободной области отрезка, упруго взаимодействуя с шариком маятника. Для введения «хаоса» в систему правая граница «флуктуирует» (ее положение случайным образом изменяется в небольшом интервале). Получить экспериментальные средние характеристики системы (энергии, координаты). Проверить теорему о равномерном распределении энергии по степеням свободы. Средняя энергия маятника имеющего две термодинамические степени свободы должна быть в два раза больше энергии свободной частицы.
Задача 6. Провести компьютерное моделирование методом Монте-Карло частицы на отрезке, который содержит потенциальную яму (канонический ансамбль). Сравнить экспериментальные средние величины (энергия, координата) с теоретическими величинами.
Задача 7. В среде MathCAD выполнить построение графиков (для различных температур) распределения Максвелла (функции плотности вероятности модуля скорости). Методом интегрирования проверить нормировку функции. Рассчитать характерные скорости молекул. Задание выполнить для воздуха (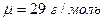
).
Задача 8. В среде MathCAD выполнить построение трехмерного графика приведенного уравнения Ван-дер-Ваальса. Получить двумерную матрицу значений давления. Провести его обработку при помощи программного модуля (обрезать по минимуму и максимуму).
Задача 9. В среде MathCAD выполнить построение графиков (для различных температур) функций Планка для теплового излучения. Проверить закон смещения Вина.
Задача 10. В среде MathCAD выполнить построение графиков функций теплоемкости кристаллов Эйнштейна и Дебая, низкотемпературной аппроксимации Дебая (кубический закон Дебая).
V. Приложение. Программы компьютерных заданий.
