Когда ставится задача имитационного моделирования некоторой сложной системы, зачастую в ней предполагается наличие случайностей. Поэтому в имитационной модели должен присутствовать блок, отвечающий за моделирование случайных величин.
Генератором (датчиком) псевдослучайных чисел называют алгоритм, который позволяет генерировать последовательность разных элементов, значения которых находятся в заданном диапазоне. Нужно четко понимать, что любой генератор дает не случайную, а детерминированную последовательность чисел.
В вычислительных машинах большее распространение получили программные методы генерации случайных чисел, которые вычисляются по формуле, и поэтому в принципиальном плане не могут являться случайными. Принято допущение, что если сгенерированные случайные числа вычисляются по специальным формулам, а ведут себя по специальным тестам, как случайные, то их можно использовать в качестве случайных.
Отличие псевдослучайных чисел от случайных заключается в том, что, начиная с некоторого времени в них наблюдается периодичность, т. е. повторение одних и тех же случайных чисел. Это существенный недостаток псевдослучайных чисел, но, с другой стороны, это дает возможность повторения одних и тех же последовательностей случайных чисел, что очень важно при проведении имитационного моделирования. На практике наиболее часто применяют следующие четыре метода генерации случайных чисел:
1. Метод квадратов: 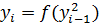 .
.
При возведении в квадрат n- разрядного числа в общем случае максимально в произведении будет 2*n разряда. В качестве i- го случайного числа берется n средних разрядов предыдущего случайного числа.
2. Метод произведений: 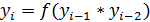 .
.
Берется n средних разрядов произведения двух предыдущих чисел.
3. Конгруэнтный метод: 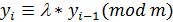 .
.
Символ 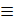 обозначает сравнимость по модулю.
обозначает сравнимость по модулю. 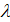 и
и 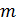 – целые положительные числа. Для получения очередного случайного числа предыдущее умножается на
– целые положительные числа. Для получения очередного случайного числа предыдущее умножается на 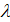 и затем делится на
и затем делится на 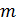 , а остаток от деления берется в качестве i- го случайного числа.
, а остаток от деления берется в качестве i- го случайного числа.
4. Смешанный конгруэнтный метод: 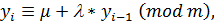 где
где
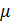 – целое положительное число. Генераторы псевдослучайных чисел современных ЭВМ, как правило, строятся на основании этого метода. Качество случайных чисел, в том числе длина периода, которая является существенным показателем качества, во многом зависит от выбранных значений
– целое положительное число. Генераторы псевдослучайных чисел современных ЭВМ, как правило, строятся на основании этого метода. Качество случайных чисел, в том числе длина периода, которая является существенным показателем качества, во многом зависит от выбранных значений 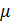 ,
, 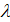 и
и 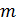 .
.
Пример 1. Рассмотрим генератор равномерно распределенных случайных чисел от 0 до 15. Для их представления требуется четыре двоичных разряда. Рассмотрим генератор с параметрами 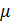 =1,
=1, 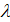 =7,
=7, 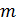 =16,
=16, 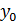 =2 и получим совокупность случайных чисел:
=2 и получим совокупность случайных чисел:
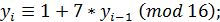
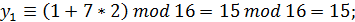
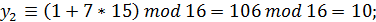
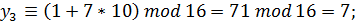
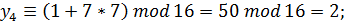
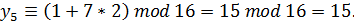
Таким образом, при выбранных параметрах смешанного конгруэнтного генератора получили длину периода, равную четырем числам.
Покажем, что при 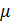 =1,
=1, 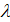 =3,
=3, 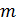 =16,
=16, 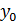 =3 длина периода удваивается:
=3 длина периода удваивается:
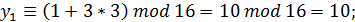
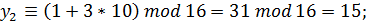
………
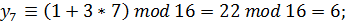
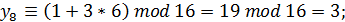
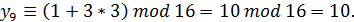
Таким образом, показано, что при данных параметрах длина периода увеличилась в два раза, и можно использовать уже 50% всех чисел, которые можно представить четырьмя двоичными разрядами.
Если в качестве значений параметров выбрать 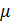 =1,
=1, 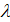 =5,
=5, 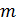 =16,
=16, 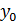 =3, то при таких значениях параметров обеспечивается период в 16 чисел, т.е. 100%-е использование совокупности чисел в четырех двоичных разрядах.
=3, то при таких значениях параметров обеспечивается период в 16 чисел, т.е. 100%-е использование совокупности чисел в четырех двоичных разрядах.
Для проверки качества последовательности равномерно распределенных случайных чисел используют три вида тестов: на равномерность, случайность и периодичность.
- Проверка равномерности. Наиболее часто используют два теста – частот и разрядов.
1) Тест частот.
Для оценки равномерности по тестам частот весь диапазон существования распределения от 0 до 1 разбивают на 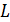 интервалов одинаковой длины и подсчитывают попадание случайной величины в каждый из них. Процедура оценки на рисунке 5 основана на использовании метода моментов (описана в главе 3).
интервалов одинаковой длины и подсчитывают попадание случайной величины в каждый из них. Процедура оценки на рисунке 5 основана на использовании метода моментов (описана в главе 3).
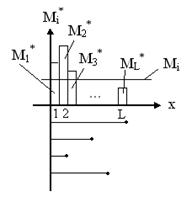
Рисунок 5. Гистограмма распределения случайной величины
Вычисляется критерий согласия 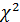 с количеством степеней свободы
с количеством степеней свободы  :
:
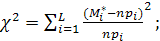
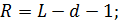
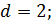
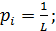
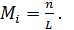 Где
Где
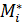 – экспериментальная
– экспериментальная 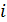 -я частота, т.е. количество попаданий случайной величины в
-я частота, т.е. количество попаданий случайной величины в 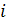 -й интервал гистограммы;
-й интервал гистограммы;
 - количество степеней свободы (разница между количеством имеющихся интервалов гистограммы и определяемыми параметрами);
- количество степеней свободы (разница между количеством имеющихся интервалов гистограммы и определяемыми параметрами);
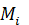 - гипотетическая частота, т.е. количество случайных чисел, которое должно было попасть в
- гипотетическая частота, т.е. количество случайных чисел, которое должно было попасть в 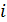 -й интервал гистограммы:
-й интервал гистограммы: 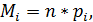 где
где
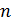 – количество реализаций случайной величины;
– количество реализаций случайной величины;
 - вероятность попадания случайной величины в
- вероятность попадания случайной величины в 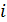 -й интервал гистограммы:
-й интервал гистограммы: 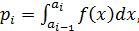 где
где
 – левая и правая границы
– левая и правая границы 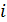 -го интервала гистограммы.
-го интервала гистограммы.
По вычисленным значениям 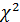 и
и  по статистическим таблицам находим коэффициент доверия гипотезе о равномерности по КС Пирсона, который должен попасть в 10%-й интервал
по статистическим таблицам находим коэффициент доверия гипотезе о равномерности по КС Пирсона, который должен попасть в 10%-й интервал 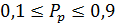 . В противном случае гипотеза отвергается.
. В противном случае гипотеза отвергается.
2) Тест разрядов.
Для равномерного закона вероятность появления любого символа в любом разряде числа одинакова. Для десятичных чисел она равна 0,1. Для двоичных – 0,5. Для проведения тестирования подсчитывается количество каждых символов в каждом разряде числа, т.е. их частоты. И аналогично предыдущему вычисляется критерий 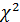 и количество степеней свободы
и количество степеней свободы  . А далее проверяется попадание коэффициента доверия гипотезе в 10%-й доверительный интервал. При отрицательном результате гипотеза отвергается.
. А далее проверяется попадание коэффициента доверия гипотезе в 10%-й доверительный интервал. При отрицательном результате гипотеза отвергается.
- Тест оценки случайности.
Для того чтобы оценить случайность, вычисляют коэффициент линейной автокорреляции, показывающий зависимость случайных чисел от ранее сгенерированных. Коэффициент автокорреляции вычисляется для последовательности случайных чисел, берущихся с некоторым шагом между собой 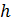 . Например, на рисунке 6 показан выбор пар чисел с шагом
. Например, на рисунке 6 показан выбор пар чисел с шагом 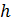 =3.
=3.
 |
x
1 2 3 4 5 6 7 8 9 10
Рисунок 6. Выбор пар чисел для вычисления коэффициента линейной автокорреляции
Коэффициент линейной автокорреляции меняется от -1 до +1 и вычисляется по формуле:
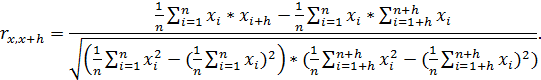
Приведем формулу для вычисления критического значения коэффициента автокорреляции: 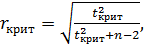 где
где
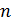 – количество пар случайных чисел;
– количество пар случайных чисел;
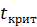 – критическое значение критерия Стьюдента, взятое по статистическим таблицам для рекомендуемого уровня значимости
– критическое значение критерия Стьюдента, взятое по статистическим таблицам для рекомендуемого уровня значимости 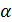 =0,05 и для количества степеней свободы
=0,05 и для количества степеней свободы 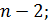
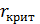 – критическое значение коэффициента линейной автокорреляции, и если вычисленное значение не меньше критического, то связь между переменными считается существенной.
– критическое значение коэффициента линейной автокорреляции, и если вычисленное значение не меньше критического, то связь между переменными считается существенной.
Если же вычисленное значение по абсолютной величине не меньше 0,8, т.е. 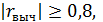 , то такая автокорреляционная связь считается близкой к линейной. На рисунке 7 представлены три вида автокорреляционной зависимости между случайными числами:
, то такая автокорреляционная связь считается близкой к линейной. На рисунке 7 представлены три вида автокорреляционной зависимости между случайными числами: 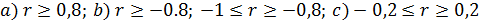 :
:
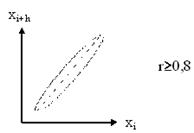
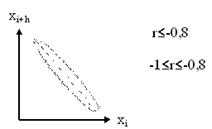
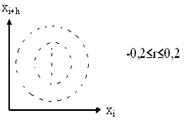
Рисунок 7. 

Для моделирования требуется использовать генераторы случайных чисел, для которых коэффициент автокорреляции не превышает 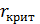 , а еще лучше не превышает
, а еще лучше не превышает 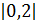 .
.
- Тест периодичности.
Тест периодичности заключается в вычислении длины периода и длины отрезка апериодичности. Период – это количество повторяющихся чисел, а отрезок апериодичности – это такая последовательность случайных чисел, в которой нет ни одной пары одинаковых чисел, но следующее число за отрезком апериодичности имеет в нем свою «пару». Для корректного проведения имитационного моделирования и получения достоверных результатов требуется использовать случайные числа только на отрезке апериодичности, потому что любое повторение случайных чисел искажает получаемые результаты.
Для вычисления длины периода используется следующий метод: генератор случайных чисел по интуиции выводится за пределы отрезка апериодичности, т.е. на совокупность случайных чисел, в которой имеются периоды. Затем запоминается очередное случайное число, а каждое последующее число сравнивается с числом, которое запомнили. Количество случайных чисел до совпадения случайного числа с числом, которое запомнили, будет являться длиной периода.
Для определения длины отрезка апериодичности берется два одинаковых генератора. После того, как первый из них выработает количество чисел, равное длине периода, запускается второй генератор, и пары вырабатываемых ими чисел сравниваются между собой до тех пор, пока сравнение не даст положительный результат. После этого подсчитывается количество чисел, выработанных первым генератором. Это и есть длина отрезка апериодичности, и чем качественнее генератор, тем больше длина его отрезка апериодичности.
 2014-02-02
2014-02-02 8217
8217
