Понятие ковариантных координат вектора
Пусть:
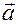 — произвольный вектор;
— произвольный вектор;
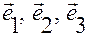 — базис основной системы координат;
— базис основной системы координат;
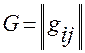 ,
, 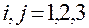 — матрица метрических
— матрица метрических
коэффициентов этой системы,
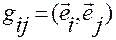 ;
;
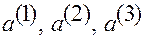 — координаты вектора
— координаты вектора 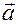 в основной
в основной
системе как отмечено выше, они
называются контравариантными
координатами вектора 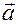 .
.
Введем следующее понятие.
Ковариантнымикоординатами вектора 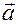 называются величины
называются величины 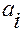 , определяемые по формуле:
, определяемые по формуле:
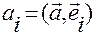 ,
, 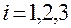 .
.
Геометрический смысл ковариантных координат вектора 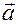 :
:
— если вектора 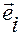 ,
, 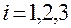 , являются ортами, то
, являются ортами, то 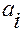 — это ортогональные проекции вектора
— это ортогональные проекции вектора 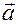 на координатные оси основной системы координат,
на координатные оси основной системы координат,
— если вектора 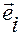 ,
, 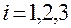 , не являются ортами, то
, не являются ортами, то 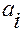 — это ортогональные проекции вектора
— это ортогональные проекции вектора 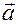 на указанные оси, умноженные на
на указанные оси, умноженные на 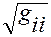 , где
, где 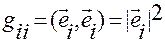 .
.
 2014-01-25
2014-01-25 692
692








