Определение 5

Связь контравариантных и декартовых координат

Связь контравариантных и криволинейных координат

Обозначим 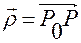радиус-вектор точки 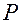относительно точки 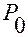(см. рис.1.5.4).

Его связь с контравариантными координатами задается разложением по векторам :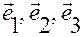

.

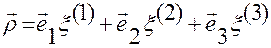Связь произвольных положений точки относительно точек отсчета и определяется соотношением

.

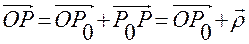В нем:

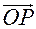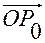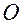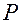и обозначают положения относительно точки отсчета точек и 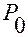, соответственно,

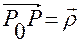— положение точки 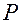относительно точки отсчета .

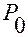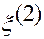
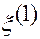
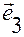
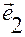
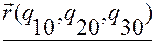
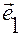
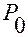
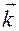
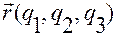
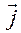
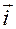
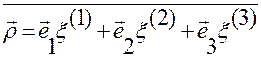
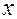Рис.1.5.4

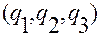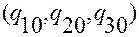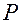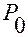Пусть и — криволинейные координаты точек и , соответственно. Тогда, согласно (1.5.1)

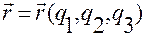, (1.5.1)

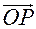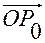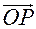
вектора и определяются равенствам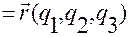и:

и .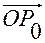

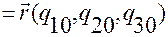Вектор 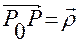, как отмечалось выше, задается разложением по векторам :

.

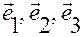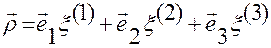Поэтому указанную связь

.

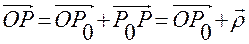можем переписать в следующей форме:

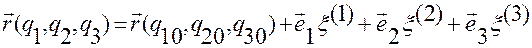(1.5.6)

Равенство (1.5.6) определяет в неявном виде зависимость обобщенных координат 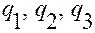точки 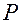от ее контравариантных координат 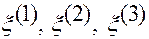и от криволинейных координат 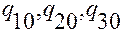точки 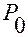, в которой построена соответствующая основная система .

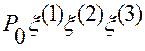Из формулы (1.5.6) легко получить связь декартовых координат 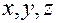с контравариантными координатами .

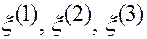Действительно, в (1.5.6) базисные вектора 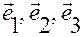основной системы вычисляются через криволинейные координаты 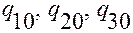точки , соответственно, по формулам:

,

, .

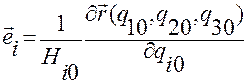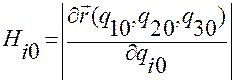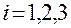Поэтому, проектируя (1.5.6)

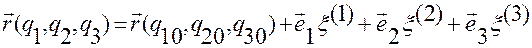(1.5.6)

на оси , , , получим искомую связь:

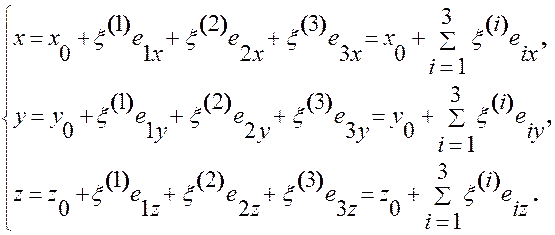
(1.5.7)

В (1.5.7) декартовые координаты 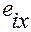, , 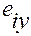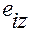векторов :

, , , ,

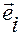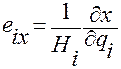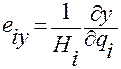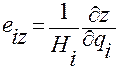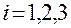вычисляются в точке ,

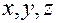— декартовые координаты точки ,

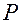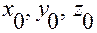— декартовые координаты точки .

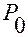В матричном виде соотношения (1.5.7) запишутся так:

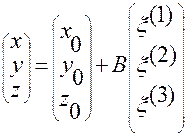, (1.5.8)

где .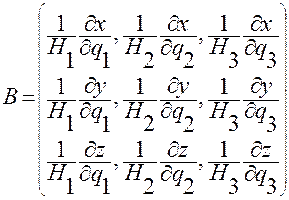

Матрица 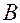называется матрицей перехода от основной системы координат к декартовой прямоугольной системе .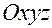

Ее элементы вычисляются через криволинейные координаты 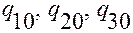точки .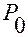

Столбцы матрицы состоят из направляющих косинусов векторов 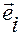относительно осей системы .

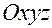Из (1.5.8) находим обратную зависимость 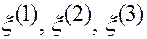от :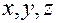

.

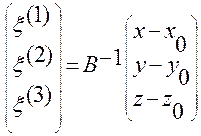Матрица 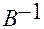называется матрицей перехода от системы 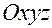к основной системе .

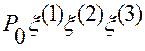4.4. Матрица метрических коэффициентов
основной системы

Установим связь матрицы 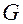метрических коэффициентов 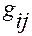, , 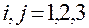основной системы координат с криволинейными координатами .

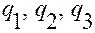Поскольку 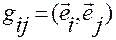, то, подставляя (1.5.5)

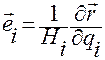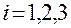, , (1.5.5)

находим

.

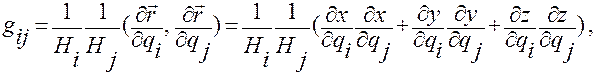
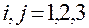Очевидно, 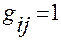при 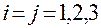, так как .

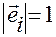Поэтому в общем случае основная система координат, построенная в любой точке 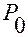, является косоугольной.

Легко видеть, что через матрицу 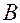матрица 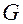может быть представлена произведением

.

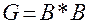Отсюда следует, в частности, что

,

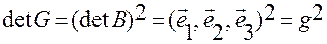где

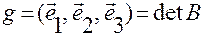
обозначает смешанное произведение векторов .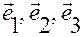

5º. Ортогональные криволинейные координаты и условия их ортогональности

Если 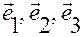взаимно ортогональные векторы, то основная система координат называется ортогональной.