2014-01-25
674
При естественном способе задания движения точки ее траектория может задаваться с использованием криволинейных координат.
Параметрическое задание траектории в таком случае имеет вид
, 
, 
, 
,
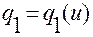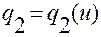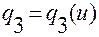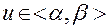где
— дважды непрерывно дифференцируемые на промежутке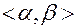 
функции.
Для того чтобы перейти к естественному способу задания движения, требуется построить естественную параметризацию траектории.
Для этого, как показано в §2, необходимо определить связь длины дуги с параметром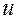 
, являющимся внутренней переменной заданной траектории.
Искомая связь будет установлена, если укажем зависимость дифференциала 
длины дуги от дифференциала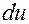 
внутренней переменной.
С целью решения поставленной задачи построим параметризацию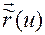 
траектории, заданной параметрически функциями .
Параметризацию 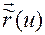получим, если подставим в (1.5.1):
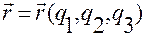(1.5.1)
вместо криволинейных координат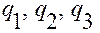 
координатные функции , соответственно.
В результате придем к следующему векторному соотношению
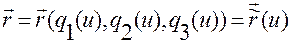, (1.5.13)
которое при каждом значении 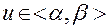задает положение в пространстве точки 
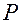, имеющей криволинейные координаты 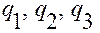на заданной траектории.
|
|
|
А тогда можем записать
,
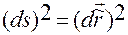где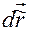 
— линейное перемещение точки 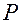по кривой .
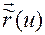Из (1.5.13) находим
,
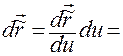
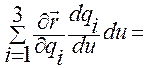
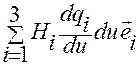и, следовательно,
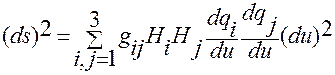. (1.5.14)
Здесь
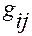— метрические коэффициенты основной
системы координат,
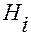и 
— коэффициенты Ламе.
Все коэффициенты вычисляются в произвольном положении точки 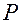на заданной кривой.
Если не фиксировать траекторию точки 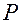(считать ее произвольной), то, учитывая, что линейное перемещение 
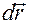связано с линейными перемещениями 
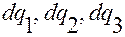криволинейных координат 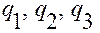соотношением
,
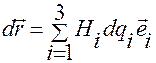получим следующее выражение для дифференциала дуги на любой траектории:
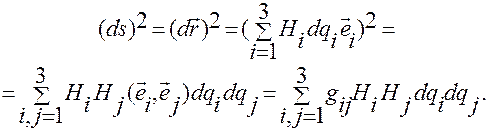
В нем следует положить
, 
, 
,
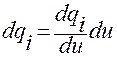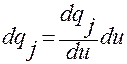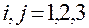в том случае, когда траектория фиксирована и определяется криволинейными координатами
, , .
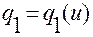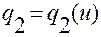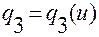В результате такой замены придем к соотношению (1.5.14)
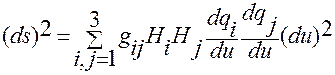. (1.5.14)
