Определение ускорений точек плоской фигуры

Рис.40

Рис.39

Рис.38

Свойства плана скоростей.

а) Стороны треугольников на плане скоростей перпендику­лярны соответствующим прямым на плоскости тела.

Действительно, 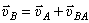. Но на плане скоростей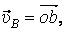 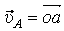. Значит 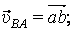причём 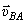перпендикулярна АВ, по­этому и 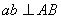. Точно так же 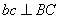и .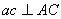

б) Стороны плана скоростей пропорциональны соответствующим от­резкам прямых на плоскости тела.

Так как , то отсюда и следует, что стороны плана скоростей пропорциональны отрезкам прямых на плоскости тела.

Объединив оба свойства, можно сделать вывод, что план скоростей подобен соответствующей фигуре на теле и повёрнут относительно её на 90˚ по направлению вращения. Эти свойства плана скоростей позволяют определять скорости точек тела графическим способом.

Пример 10. На рисунке 39 в масштабе изображён механизм. Известна угловая скорость 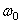звена ОА.

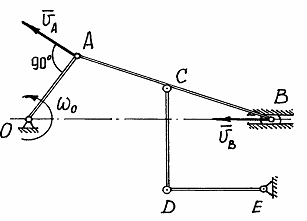
Чтобы построить план ско­ростей должна быть известна скорость какой-нибудь одной точки и хотя бы направление вектора скорости другой. В на­шем примере можно определить скорость точки А: 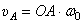и направление её вектора .

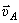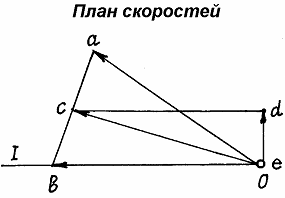
Откладываем (рис. 40) из точки о в масштабе 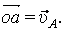Известно направление вектора скорости ползуна В – горизонтальное. Проводим на плане скоростей из точки О прямую I по направлению скорости 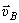, на которой должна находиться точка b, определяющая скорость этой точки В. Так как стороны плана скоростей перпендикулярны соответствующим звеньям механизма, то из точки а проводим прямую перпендикулярно АВ до пересечения с прямой I. Точка пересечения определит точку b, а значит и скорость точки В: 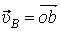. По второму свойству плана скоростей его стороны подобны звеньям механизма. Точка С делит АВ пополам, значит и с должна делить аb пополам. Точка с определит на плане скоростей величину и направление скорости 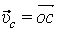(если с соединить с точкой О).

Скорость точки Е равна нулю, поэтому точка е на плане скоростей совпадает с точкой О.

Далее. Должно быть 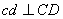и 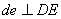. Проводим эти прямые, находим их точку пересечения d. Отрезок оd определит вектор скорости .

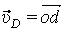Покажем, что ускорение любой точки М плоской фигуры (так же, как и скорость) складывается из ускорений, которые точка получает при поступательном и вращательном движениях этой фигуры. Положение точки М по отношению к осям Оxy (см.рис.30) определяется радиусом-вектором 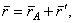где 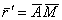. Тогда

.

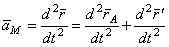В правой части этого равенства первое слагаемое есть ускорение 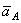полюса А, а второе слагаемое определяет ускорение 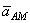, которое точка м получает при вращении фигуры вокруг полюса A. следовательно,

.

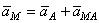Значение 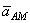, как ускорения точки вращающегося твердого тела, определяется как

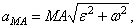
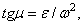
где 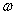и 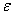- угловая скорость и угловое ускорение фигуры, а 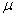- угол между вектором 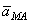и отрезком МА (рис.41).

Таким образом, ускорение любой точки М плоской фигуры геометрически складывается из ускорения какой-нибудь другой точки А, принятой за полюс, и ускорения, которое точка М получает при вращении фигуры вокруг этого полюса. Модуль и направление ускорения 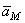, находятся построением соответствующего параллелограмма (рис.23).

Однако вычисление 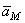с помощью параллелограмма, изображен­ного на рис.23, усложняет расчет, так как предварительно надо бу­дет находить значение угла 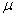, а затем - угла между векторам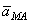и и 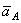, Поэтому при решении задач удобнее вектор 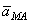заменять его касательной 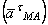и нормальной 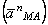составляющими и пред­ставить в виде