Рис.44
Рис.43
Угловую скорость находим с помощью мгновенного центра скоростей:
Рис. 9.29.
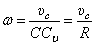 .
.
Угловое ускорение при таком движении можно найти как производную от угловой скорости. Имея в виду, что 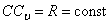 , а точка С движется по прямой, получим
, а точка С движется по прямой, получим
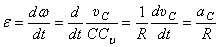 .
.
Если С – полюс, то 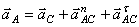 , где
, где
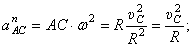
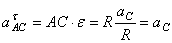 .
.
Величину ускорения найдём с помощью проекций на оси х и у:
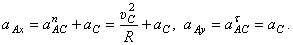
Тогда 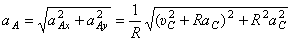 .
.
Ускорение мгновенного центра скоростей 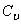 :
: 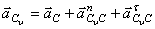 ,
,
где 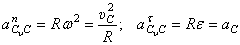 .
.
И, так как 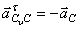 , ускорение
, ускорение 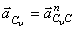 и
и 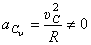 .
.
Таким образом, ускорение мгновенного центра скоростей не равно нулю.
Пример 12. Вернёмся к примеру 9 (рис. 44).
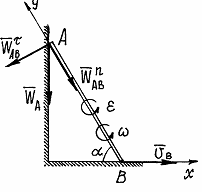
Найдём ускорение точки А, полагая 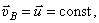 т.е.
т.е. 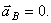
Имеем:
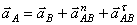 , (1)
, (1)
где 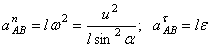 , но направление вектора
, но направление вектора 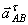 неизвестно, неизвестно и угловое ускорение
неизвестно, неизвестно и угловое ускорение 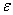 .
.
Предположим, что вектор 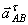 направлен перпендикулярно АВ, влево.
направлен перпендикулярно АВ, влево.
Ускорение 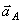 , конечно, направлено по траектории прямолинейного движения точки А, предположим вниз. Спроектируем векторное равенство (1) на оси х и у, получим:
, конечно, направлено по траектории прямолинейного движения точки А, предположим вниз. Спроектируем векторное равенство (1) на оси х и у, получим:
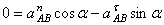 и
и 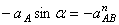 .
.
Из второго уравнения сразу находим ускорение точки А
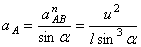 .
.
Положительное значение 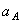 указывает на то, что направление вектора
указывает на то, что направление вектора 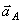 выбрано правильно.
выбрано правильно.
Из первого уравнения можно найти ускорение 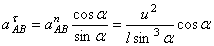 и угловое ускорение
и угловое ускорение 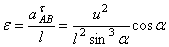 (направления
(направления 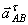 и
и 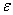 также угаданы верно).
также угаданы верно).
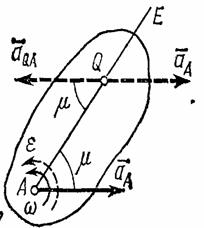
При непоступательном движении плоской фигуры у нее в каждый момент времени имеется точка Q, ускорение которой равно нулю. Эта точка называется мгновенным центром ускорений. Определяется положение центра Q, если известны ускорение 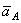 какой-нибудь точки А фигуры и величины
какой-нибудь точки А фигуры и величины 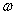 и
и 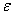 , следующим путем:
, следующим путем:
1) находим значение угла 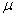 , из формулы
, из формулы 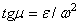 ;
;
2) от точки А под углом 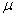 , к вектору
, к вектору 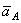 проводим прямую АЕ (рис.45);
проводим прямую АЕ (рис.45);
при этом прямая АЕ должна быть отклонена от 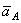 в сторону вращения фигуры, если вращение является ускоренным, и против вращения, если оно является замедленным, т. е. в сторону направления углового ускорения
в сторону вращения фигуры, если вращение является ускоренным, и против вращения, если оно является замедленным, т. е. в сторону направления углового ускорения 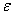 ;
;
3) откладываем вдоль линии АЕ отрезок AQ, равный
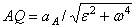 .
.
 2014-01-25
2014-01-25 725
725








