Одной из основных характеристик движения точки является ее скорость относительно выбранной системы отсчета.
Скорость точки при векторном способе задания движения
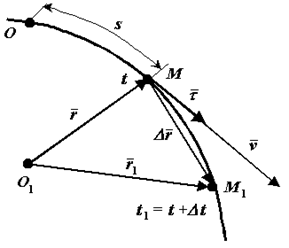
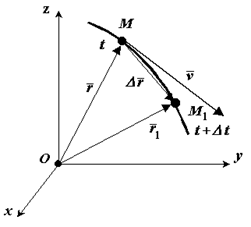 Положение движущейся точки М относительно системы отсчета в момент времени
Положение движущейся точки М относительно системы отсчета в момент времени 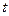 определяется радиус-вектором
определяется радиус-вектором 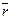 . В другой момент времени
. В другой момент времени 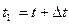 точка займет положение М 1 с радиус-вектором
точка займет положение М 1 с радиус-вектором 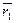 . За время
. За время 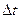 радиус-вектор движущейся точки изменится на
радиус-вектор движущейся точки изменится на 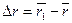 .
.
Средней скоростью 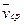 называется отношение изменения радиус-вектора
называется отношение изменения радиус-вектора 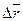 к изменению времени
к изменению времени 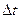 .
.
Рис. 1.4 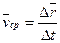 (1-4)
(1-4)
Скорость точки равна первой производной по времени от ее радиус-вектора.
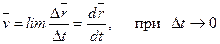 (1-5)
(1-5)
Скорость точки при координатном способе задания движения
Разложим радиус-вектор и скорость на составляющие, параллельные осям координат. Получим
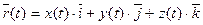
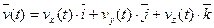 (1-6)
(1-6)
После дифференцирования
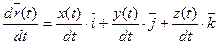 (1-7)
(1-7)
Отсуда следует
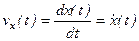
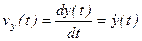
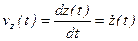 (1-8)
(1-8)
Проекция скорости точки на какую-либо координатную ось равна первой производной по времени от соответствующей координаты этой точки.
Модуль скорости и направляющие косинусы равны:
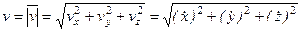
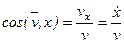
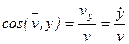
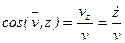
Если точка движется в плоскости, то, выбрав оси координат Ox и Oy в этой плоскости, получим:
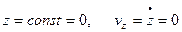
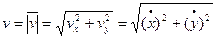
Для прямолинейного движения точки координатную ось, например ось Ox, направляем по траектории. Тогда
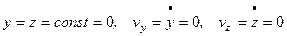
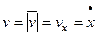
Скорость точки при естественном способе задания движения.
Пусть скорость точки задана естественным способом, т.е. заданы траектория точки и закон ее движения по траектории 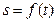 .
.
 Вычислим скорость точки.
Вычислим скорость точки.
Используем радиус-вектор 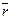 . движущейся точки, начало которого находится в неподвижной точке
. движущейся точки, начало которого находится в неподвижной точке 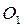
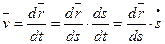
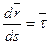 - единичный вектор, направленный по касательной к траектории в сторону возрастающих расстояний.
- единичный вектор, направленный по касательной к траектории в сторону возрастающих расстояний.
Рис. 1.5
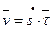 (1-9)
(1-9)
При 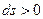 направления векторов
направления векторов 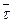 и
и 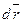 совпадают. Если точка движется в сторону убывающих расстояний, то
совпадают. Если точка движется в сторону убывающих расстояний, то 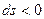 и направления векторов
и направления векторов 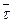 и
и 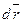 противоположны.
противоположны.
При 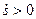 вектор скорости направлен по
вектор скорости направлен по 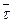 , т.е. в сторону возрастающих расстояний; при
, т.е. в сторону возрастающих расстояний; при 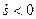 он имеет направление, противоположное
он имеет направление, противоположное 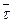 , т.е. в сторону убывающих расстояний.
, т.е. в сторону убывающих расстояний.
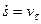 - алгебраическая скорость точки, проекция скорости
- алгебраическая скорость точки, проекция скорости 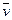 на положительное направление касательной к траектории.
на положительное направление касательной к траектории.
Естественное задание движения точки полностью определяет скорость по величине и направлению.
 2014-01-25
2014-01-25 717
717








