Рис.42
Проведем теперь через любую точку O 1 на оси z плоскость ху, перпендикулярную к оси; проектируя силу 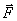 на эту плоскость, найдем
на эту плоскость, найдем 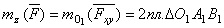 .
.
Но треугольник О 1 А 1 В 1 представляет собою проекцию треугольника ОАВ на плоскость ху. Угол между плоскостями этих треугольников равен углу между перпендикулярами к плоскостям, т. е. равен 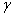 . Тогда, по известной геометрической формуле,
. Тогда, по известной геометрической формуле, 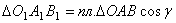 .
.
Умножая обе части этого равенства на 2 и замечая, что удвоенные пощади треугольников О 1 А 1 В 1 и ОАВ равны соответственно m z(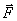 ) и
) и 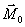 , найдем окончательно:
, найдем окончательно: 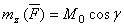 .
.
Так как произведение 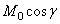 дает проекцию вектора
дает проекцию вектора 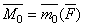 на ось z, то равенство можно еще представить в виде
на ось z, то равенство можно еще представить в виде
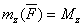 или
или 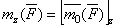 .
.
В результате мы доказали, что между моментом силы относительно оси и ее моментом относительно какого-нибудь центра, лежащего на этой оси, существует следующая зависимость: момент силы 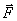 относительно оси равен проекции на эту ось вектора, изображающего момент данной силы относительно любого центра, лежащего на оси.
относительно оси равен проекции на эту ось вектора, изображающего момент данной силы относительно любого центра, лежащего на оси.
Полученные выше результаты позволяют решить задачу о приведении любой системы сил к данному центру. Эта задача, решается с помощью теоремы о параллельном переносе силы. Для переноса действующей на абсолютно твердое тело силы 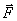 из точки А (рис. 43, а) в точку О прикладываем в точке О силы
из точки А (рис. 43, а) в точку О прикладываем в точке О силы 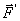 =
= 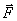 и
и 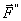 = -
= -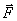 . Тогда сила
. Тогда сила 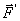 =
= 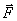 окажется приложенной в точке О и к ней будет присоединена пара (
окажется приложенной в точке О и к ней будет присоединена пара (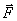 ,
, 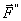 ) с моментом
) с моментом 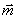 , что можно показать еще так, как на рис. 43, б. При этом
, что можно показать еще так, как на рис. 43, б. При этом 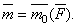
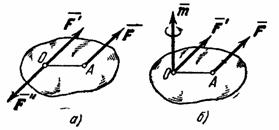
 2014-01-25
2014-01-25 726
726








