Простейшие теоремы статики

Теорема о переносе силы вдоль линин действия. Действие силы на твердое тело не изменится от переноса силы вдоль своей линии действия.

Пусть в точке А твердого тела приложена сила 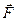(рис. 3). На ее линии действия в точке В в соответствии с аксиомой II добавим систему сил 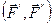эквивалентную нулю, для которой .

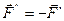Выберем силу 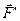, равную силе 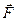. Полученная система трех сил 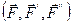эквивалентна, соглано аксиоме о добавлении равновеснои системы сил, силе 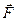, т. е.

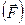P .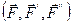

Система сил 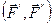, согласно аксиоме I, эквивалентна нулю и, согласно аксиоме II, ее можно отбросить. Получится одна сила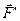, приложенная в точке В, т. е. 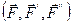P 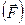. Окончательно получаем

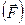P .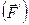

Сила 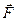приложена в точке А.

Сила, приложенная к твердому телу, есть вектор скользящий, т. е. его можно переносить по линиии действия.

Теорема о трех силах. Если твердое тело под действием трех сил, две из которых пересекаются в одной точке, находится в равновесии, то линии действия таких трех сил пересекаются в одной точке, а силы располагаются в одной плоскости.

Обратная теорема не верна.

Пусть имеем систему трех сил 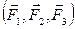, две из которых, например 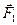и 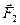, пересекаются в одной точке А (рис. 4). Докажем, что если тело находится в равновесии под действием этих трех сил, то линия действия силы 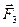пройдет через точку А, т. е. линии действия трех сил пересекаются в одной точке.

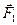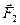Силы и , линии действия которых пересекаются в точке А, перенесем в эту точку и заменим их равнодействующей 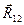по аксиоме параллелограмма сил. Система трех сил 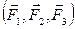свелась к эквивалентной системе двух сил 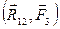, находящихся в равновесии, так как твердое тело, на которое они действуют, по условиям теоремы находится в равновесии. Согласно аксиоме I, такие две силы должны быть направлены по одной прямой, проходящей через точки их приложения. Следовательно, линия действия силы 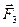должна пройти через точку приложения силы 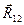, т. е. точку пересечения сил 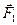и 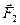. Таким образом, три силы пересекутся в однои точке.