Аксиомы статики

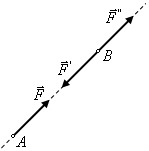
I. 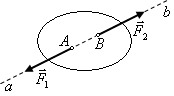Аксиома о равновесии системы двух сил. Для равновесия системы двух сил, приложенных к точкам твердого тела, необходимо и достаточно, чтобы эти силы были равны по, модулю и действовали вдоль одной прямой, проходящей через точки их приложения, в противоположных направлениях (рис. 1).

II. Аксиома о добавлении (отбрасывании) системы сил, эквивалентной нулю. Если на твердое тело действует система сил, то к ней можно добавить (отбросить) эквивалентную нулю. Полученная после добавления (отбрасывания) новая система сил является эквивалентной первоначальной системе сил.

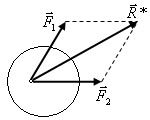
III. Аксиома параллелограмма сил. Две силы, действующие в одной точке твердого тела или на одну материальную точку, можно заменить одной равнодействующей силой, равной по модулю и направлению диагонали параллелограмма, построенного на заданных силах (рис. 2).

Очевидно, справедливо и обратное. Одну силу, приняв за равнодействующую, можно разложить по правилу параллелограмма на две составляющие.

Замену двух сил одной равнодействующей силой по правилу параллелограмма называют векторным сложением этих сил.

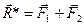Модуль равнодействующей силы R* как векторную сумму сил вычисляют по формуле диагонали параллелограмма

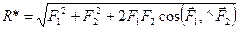IV. Аксиома о равенстве сил действия и противодействия – закон Ньютона: всякой силе действия есть равная, но противоположная сила противодействия.

V. Аксиома связей. Связью для твердого тела или материальной точки называют материальные объекты, которые ограничивают свободу перемещения рассматриваемого твердого тела. Аксиома связей утверждает, что всякую связь можно отбросить и заменить силой, реакцией связей (в простейшем случае) или системой сил (в общем случае).

VI. Аксиома затвердевания. Если деформируемое тело находится в равновесии, то равновесие его без изменения системы приложенных сил не нарушится от наложения на точки тела дополнительных связей, включая превращение деформируемого тела в абсолютно твердое.