Дана табличная функция, т.е. дана таблица, в которой для некоторых дискретных значений аргумента xi, расположенных в порядке возрастания, заданы соответствующие значения функции уi:
| i | x | y |
| 0 | x0 | y0 |
| 1 | x1 | y1 |
| 2 | x2 | y2 |
| ... | ... | ... |
| i | xi | yi |
| ... | ... | ... |
| n | xn | yn |
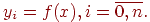
| (11.1) |
Точки с координатами (xi, yi) называются узловыми точками или узлами.
Количество узлов в табличной функции равно
N=n+1.На графике табличная функция представляется в виде совокупности узловых точек (рис. 11.1).
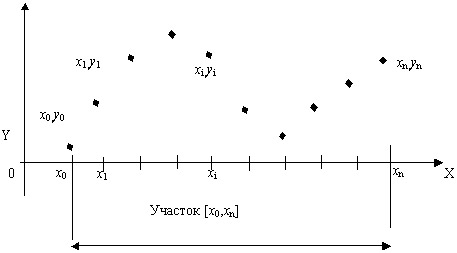
Рис. 11.1.
Длина участка [x0, xn] равна (xn - x0).
В расчетной практике инженера часто возникают задачи найти значение функции для аргументов, которые отсутствуют в таблице. Такие задачи называются задачами интерполирования или экстраполирования.
Задача интерполирования функции (или задача интерполяции) состоит в том, чтобы найти значения yk табличной функции в любой промежуточной точке хк, расположенной внутри интервала [x0, xn], т.е.
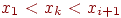
и
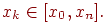
Задача экстраполирования функции (или задача экстраполяции) состоит в том, чтобы найти значения yl табличной функции в точке хl, которая не входит в интервал [x0, xn], т.е.
|
|
|
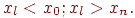
Такую задачу часто называют задачей прогноза.
Обе эти задачи решаются при помощи нахождения аналитического выражения некоторой вспомогательной функции F(x), которая приближала бы заданную табличную функцию, т.е. в узловых точках принимала бы значение табличных функций
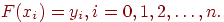
Для определенности задачи искомую функцию F(x) будем искать из класса алгебраических многочленов:
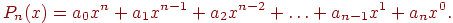
| (11.2) |
Этот многочлен должен пройти через все узловые точки, т.е.
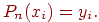
| (11.3) |
Поэтому степень многочлена n зависит от количества узловых точек N и равна количеству узловых точек минус один, т.е. n=N-1.
Многочлен вида (11.2), который проходит через все узловые точки табличной функции называется интерполяционным многочленом.
Интерполирование с помощью алгебраических многочленов называется параболическим интерполированием.
Таким образом, для решения задачи интерполирования прежде всего необходимо решить задачу, которую можно сформулировать следующим образом:
для функции 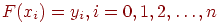 , заданной таблично, построить интерполяционный многочлен степени n, который проходит через все узловые точки таблицы:
, заданной таблично, построить интерполяционный многочлен степени n, который проходит через все узловые точки таблицы:
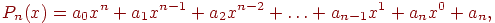
где
n-степень многочлена, равная количеству узловых точек N минус один,т.е. n=N-1.
В результате, в любой другой промежуточной точке хk, расположенной внутри отрезка [x0,xn] выполняется приближенное равенство Pn(xk) f(xk) yk. (рис.11.2)
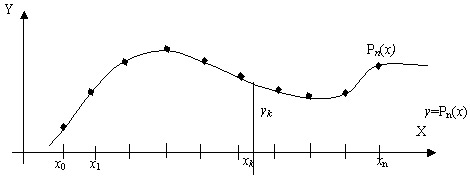
Рис. 11.2.
 2018-02-23
2018-02-23 706
706








