Решение систем нелинейных уравнений методом Ньютона

Дана система нелинейных уравнений

(10.5)

или

Необходимо решить эту систему, т.е. найти вектор , удовлетворяющий систему (10.5) с точностью .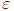

Метод Ньютона наиболее распространенный метод решения систем нелинейных уравнений. Он обеспечивает более быструю сходимость по сравнению с методом итераций.

В основе метода Ньютона лежит идея линеаризации всех нелинейных уравнений системы (10.5). Сообщим всей системе (10.5) малые приращения h_j и разложим каждое уравнение системы (10.5) в ряд Тейлора:

(10.6)

где

h_j- приращение по каждой x_j;

R_i - остаточные нелинейные члены второго и более высоких порядков каждого ряда Тейлора.

Если приращения h_j таковы, что переменные x_j принимают значения близкие к корню, то будем считать, что левые части уравнений системы (10.6) обращаются в нули. Тогда отбросив R_i сведем задачу решения системы нелинейных уравнений (10.5) к решению системы линейных уравнений, в которой неизвестными являются приращения h_j,

(10.7)

Система (10.7) – система линейных уравнений с неизвестными h_j, . Запишем (10.7) в матричной форме

где

(3.3)

(10.7)

Матрица А, составленая из частных производных ; называется матрицей Якоби или Якобианом.

Метод Ньютона состоит из двух этапов:

На первом этапе реализации метода Ньютона необходимо построить систему (11.3).

На втором этапе, начиная с начальной точки , необходимо решать систему (11.3) на каждом шаге итерационного процесса поиска методом Гаусса. Найденные значения приращений h_j используются как поправки к решению, полученному на предыдущем шаге поиска, т.е.