2018-02-13
398
Лабораторна установка (рис.16.2) складається з двох зв'язаних пружинами 10, 11 маятників 8, 9, кожен з яких коливається у своїй вертикальній площині. Для підтримки незгасаючих коливань використовується важіль зовнішньої сили 7, зв'язаний з електричним двигуном. Установка має індикатор часу 17 та індикатор кількості коливань 18. На передній панелі є кнопка вимикача струму "ПУСК" і кнопка стирання показів шкали 19, кнопка "СТОП", вмикач двигуна 15, регулятор числа обертів двигуна 16, індикатор роботи двигуна.
|
|
Система маятників установки має два ступені вільності. При малих коливаннях можна знехтувати вертикальними зміщеннями точок маятників і розглядати їх рух вздовж однієї горизонтальної прямої. Положення точок, що коливаються (центри мас маятників) характеризуються зміщеннями х 1 та х 2 від своїх положень рівноваги, позначених буквами О1 та О2 на рис.16.3. Коли точки знаходяться одночасно в положенні рівноваги, пружина, що їх з'єднує, не деформується і тому не діє на точки з якимись силами.
Рівняння руху маятників, без врахування їх зв'язку через пружину або у випадку, коли пружина не деформується, мають вигляд:
(16.6)
При деформації пружини виникають сили F, пропорційні її видовженню або стиску (закон Гука), і тому рівняння (16.6) вже не дорівнюють 0, а прирівнюються до цієї зовнішньої пружної сили. У випадку, якщо б пружина була прикріплена до центра мас маятників, то видовження пружини було б D х = х 2 – х 1 (див. рис.16.3) і тому сили, що діють на маятники, рівні:
, (16.7)
де k - коефіцієнт жорсткості пружини. Тому рівняння руху з врахуванням сил зв'язку через деформацію пружини мають вигляд:
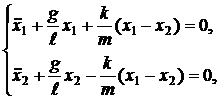(16.8)
де m однакова маса маятників, зосереджена в центрі мас. Складаючи і віднімаючи рівняння системи (16.8), одержуємо два нових рівняння, що описують нормальні гармонічні коливання:
; (16.9)
.
Як видно із системи рівнянь (16.9), частоти однофазних і протифазних нормальних коливань задаються відповідно виразами:
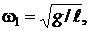(16.10)
(16.11)
У виводі, приведеному вище, допускалося, що пружина з'єднує центри мас маятників. Якщо вона розмішена на віддалі 
від точки підвісу (тобто так, як і зображено на рис. 16.3), то частота протифазних коливань w2 задається виразом:
(16.12)
Це зумовлено тим, що видовження пружини стає іншим, а саме D х ¢=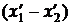 
(рис.16.3). Рівняння нормальних коливань (16.9) тоді перепишуться так:
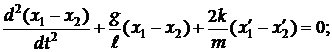(16.13)
Через те, що 
(із подібності трикутників (рис.16.3)), то
(16.14)
Підставляючи (16.14) у друге рівняння системи (16.13) і порівнюючи одержане рівняння з диференціальним рівнянням для гармонічних коливань, одержуємо рівність (16.12). Формули (16.10) і (16.12) є кінцеві робочі формули. За цими формулами можуть бути розраховані однофазні і протифазні коливання, які, у свою чергу, можуть бути одержані експериментально.
