Алгоритм для решения системы линейных уравнений методом Гаусса

Выражаем первое неизвестное из первого уравнения и подставляем его в остальные уравнения.

1. Получаем новую систему, в которой число уравнений и неизвестных на 1 меньше.

2. С новой системой поступаем таким же образом и так продолжаем до тех пор, пока не останется одно линейное уравнение, которое легко решается.

3. Когда получено значение последнего неизвестного x_n, подставляем его в уравнение, которое позволяет найти x_{n – 1} по x_n.

4. По найденным x_{n – 1} и x_n находим x_{n – 2} и таким образом находим последовательно все неизвестные.

Для систем нелинейных уравнений этот метод не всегда применим уже в силу того, что из уравнений системы совсем не обязательно можно будет выразить одну неизвестную через остальные.

Основные понятия

Квадратное уравнение с действительными коэффициентами и отрицательным дискриминантом не имеет действительных корней. Поэтому приходится расширять множество действительных чисел, добавляя к нему новые числа. Эти новые числа вместе с действительными числами образуют множество, которое называют множеством комплексных чисел.

Комплексное число – это выражение вида

, (1.1)

где x, y – вещественные числа, а – мнимая единица. Первое из вещественных чисел, x, называется вещественной (действительной) частью комплексного числа (используется обозначение 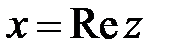); второе, y, - мнимой частью (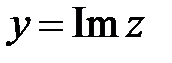). Выражение (1.1) называют алгебраической формой записи комплексного числа.

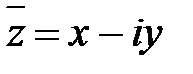Числом, сопряженным к , называют число вида . Используя формулу разности квадратов, получаем, что . Можно доказать, что корнями квадратного уравнения с отрицательным дискриминантом являются два сопряженных комплексных числа.

Тригонометрическая форма комплексного числа. Каждому комплексному числу вида (1.1) можно поставить в соответствие точку M(x;y) на декартовой плоскости (при этом на оси OX располагаются вещественные числа , а на оси OY – чисто мнимые числа ).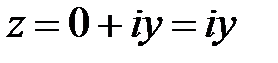

Модулем комплексного числа назовем длину отрезка (или расстояние от начала координат до точки M), т.е. . Аргументом комплексного числа () назовем угол, который вектор образует с положительным направлением оси OX. Главное значение аргумента, которое, как правило, используется при осуществлении действий с комплексными числами, удовлетворяет условию . При этом выражение вида

(1.2)

называется тригонометрической формой записи комплексного числа.

Преобразуем (1.1)

и, сравнивая с (1.2), получаем, что аргумент z можно найти, решив систему

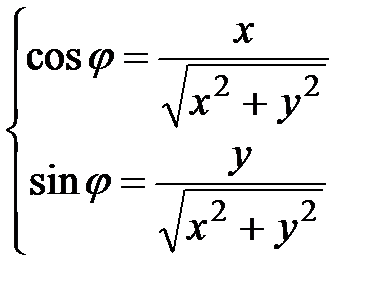или (1.3.)

Возведение в степень и извлечение корней. Если комплексное число задано тригонометрической формой , то справедлива формула Муавра

. (1.4)

Для извлечения корня n -й степени (n – целое число, большее 1) из комплексного числа, заданного в тригонометрической форме, применяется формула, дающая n значений этого корня:

, k=0,1,…,n-1. (1.5)