Метод коррелирования разностей, когда коррелируют разности уровней – первые, вторые и так далее.
При линœейной тенденции рассчитывают только первые разности – абсолютные приросты уровней:
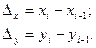
Затем рассчитывают коэффициент корреляции разностей:
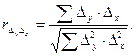
Он принимает значения от -1 до 1 и интерпретируется аналогично коэффициенту корреляции отклонений.
При параболической тенденции на основе первых разностей рассчитывают вторые:
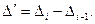
Затем в формулу для расчета коэффициента корреляции вместо первых разностей подставляют вторые.
46. Методы устранения автокорреляции: метод коррелирования отклонений уровня ряда от основных тенденций
Метод коррелирования отклонений, когда коррелируют не сами уровни, а их отклонения от основной тенденции, а при ее отсутствии – от среднего уровня.
Вначале для каждого ряда определяют уравнение тренда или средний уровень. Затем из фактических уровней вычитают уровни тренда или средний уровень:
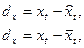

Далее оценивают тесноту связи между рядами, рассчитывая коэффициент корреляции отклонений:
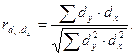
Его величина изменяется от -1 до 1. Знак указывает на направление связи: отрицательный – обратная, положительный – прямая. Чем ближе абсолютное значение этого коэффициента к 1, тем сильнее связь.
47. Понятие дисперсионного анализа, его сущность и задачи
Дисперсионный анализ — метод в математической статистике, направленный на поиск зависимостей в экспериментальных данных путём исследования значимостиразличий в средних значениях[1][2]. В отличие от t-критерия, позволяет сравнивать средние значения трёх и более групп. Разработан Р. Фишером для анализа результатов экспериментальных исследований. Суть дисперсионного анализа сводится к изучению влияния одной или нескольких независимых переменных, обычно именуемых факторами, на зависимую переменную. Зависимые переменные представлены значениями абсолютных шкал (шкала отношений). Независимые переменные являются номинативными (шкала наименований), то есть отражают групповую принадлежность, и могут иметь две или более градации (или уровня). Примерами независимой переменной {\displaystyle X_{i}}с двумя градациями могут служить пол (женский: {\displaystyle X_{1}}Х1, мужской: {\displaystyle X_{2}}Х2) или тип экспериментальной группы (контрольная: {\displaystyle X_{1}}Х1, экспериментальная: {\displaystyle X_{2}}Х2). Градации, соответствующие независимым выборкам объектов, называются межгрупповыми, а градации, соответствующие зависимым выборкам, — внутригрупповыми.
Обобщенно задача дисперсионного анализа состоит в том, чтобы из общей вариативности признака выделить три частные вариативности:
- Вариативность, обусловленную действием каждой из исследуемых независимых переменных.
- Вариативность, обусловленную взаимодействием исследуемых независмых переменных.
- Вариативность случайную, обусловленную всеми неучтенными обстоятельствами.
Вариативность, обусловленная действием исследуемых переменных и их взаимодействием соотносится со случайной вариативностью. Показателем этого соотношения является F – критерий Фишера (метод, не имеющий ничего общего, кроме автора, с «угловым преобразованием Фишера»).
FэмпА = Вариативность, обусловленная действием переменной А / Случайная вариативность
FэмпБ = Вариативность, обусловленная действием переменной Б / Случайная вариативность
FэмпАБ = Вариативность, обусловленная взаимодействием А и Б / Случайная вариативность
48. Разложение общей суммы квадратов в однофакторном дисперсионном анализе. Оценка дисперсий
В случае выделения групп по одному фактору мы имеем так называемый однофакторныйдисперсионный комплекс. Разложение дисперсии при этом производится в соответствии справилом сложения дисперсий (см. гл. б):
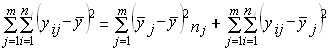 ,
,
где уij - значение результативного признака у i-й единицы в j-й группе;
i - номер единицы, i = 1,.... п.;
j - номер группы;
пj- численность у-й группы;
yj - средняя величина результативного признака в у-й группе;
у? — общая средняя результативного признака.
Если обозначить суммы квадратов отклонений буквой D, получим равенство:
Dобщ = Dфакт +Dост (7.41)
На основе разложения дисперсии (7.41) в соответствии с гипотезой отсутствия различий междугруппами могут быть получены три оценки генеральной дисперсии, пропорциональные степенисвободы: на основе общей вариации, межгрупповой (факторной) и внутригрупповой(остаточной). Число степеней'свободы равно:
для общей вариации 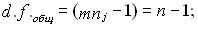
для межгрупповой вариации 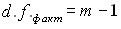 ;
;
для внутригрупповой вариации 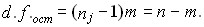
Как и суммы квадратов отклонений, числа степеней свободы связаны между собой равенством:
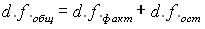
или
п - 1 = (m - 1) + (п - т). (7.42)
Деление сумм квадратов отклонений на соответствующее число степеней свободы дает триоценки генеральной дисперсии σ2.
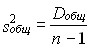 ,
,
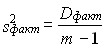 , (7.43)
, (7.43)
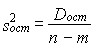 .
.
Поскольку Dфакт измеряет вариацию результативного признака, связанную с изменениемфактора, по которому произведена группировка, a Dост - вариацию, связанную с изменениемвсех прочих факторов, сравнение этих величин, рассчитанных на одну степень свободы, даетвозможность оценить существенность влияния признака-фактора на результативный признак спомощью F-критерия:
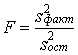 .
.
Эта запись предполагает, что s2факт > s2ост. Как правило, мы получаем именно такоесоотношение. Если F факт >Fтабл (α., d.f.1, d.f.2), можно утверждать, что нуль-гипотеза несоответствует фактическим данным, влияние признака-фактора является существенным или, иначе говоря, статистически значимым
ОЦЕНКА ДИСПЕРСИИ
На первый взгляд наиболее естественной оценкой представляется
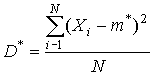 | (3) |
где 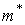 вычисляется по формуле (2). Проверим, является ли оценка
вычисляется по формуле (2). Проверим, является ли оценка 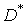 несмещенной. Формула (3) может быть записана следующим образом [1]:
несмещенной. Формула (3) может быть записана следующим образом [1]:
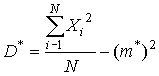 .
.
Подставим в эту формулу выражение (2):
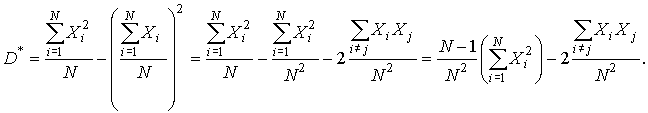
Найдем математическое ожидание оценки дисперсии:
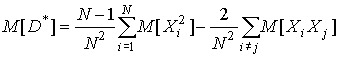 | (4) |
Так как дисперсия случайной величины не зависит от того, какое математическое ожидание у случайной величины, примем математическое ожидание равным 0, т.е. m = 0.
Тогда
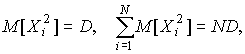 | (5) |
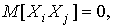 при при 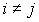 . . | (6) |
Последнее равенство следует из того, что эксперименты независимы, а математическое ожидание случайной величины в каждом эксперименте равно 0. Подставляя (5) и (6) в (4), получим:
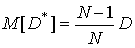
Отсюда следует, что оценка 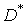 не является несмещенной - ее математическое ожидание равно не D, а несколько меньше. Пользуясь оценкой
не является несмещенной - ее математическое ожидание равно не D, а несколько меньше. Пользуясь оценкой 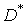 вместо дисперсии D, мы получим систематическую ошибку. Чтобы ликвидировать это смещение, достаточно ввести поправку, умножив величину
вместо дисперсии D, мы получим систематическую ошибку. Чтобы ликвидировать это смещение, достаточно ввести поправку, умножив величину 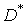 на (N-1)/N. Такую исправленную статистическую дисперсию мы и выберем в качестве оценки:
на (N-1)/N. Такую исправленную статистическую дисперсию мы и выберем в качестве оценки:
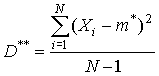
Таким образом, если в результате N экспериментов мы располагаем набором N значений случайной величины
x1, x2, …, xN,
то для оценок математического ожидания и дисперсии необходимо воспользоваться следующими формулами:
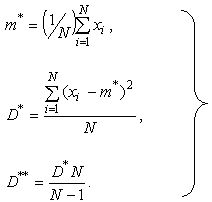 |
49. Понятие системы одновременных регрессионных уравнений: общий вид, модель спроса-предложения
50. Методы оценивания параметров структурной модели: косвенный МНК, двухшаговый МНК, трехшаговый МНК, метод максимального правдоподобия
 2018-02-13
2018-02-13 883
883







