Приближенные вычисления с помощью полного дифференциала

           Пусть функция f(x, y) дифференцируема в точке (х, у). Найдем полное приращение этой функции:

           Если подставить в эту формулу выражение

то получим приближенную формулу:

Производная и дифференциал сложной функции.

 

Производная сложной функции.

           Теорема. Пусть y = f(x); u = g(x), причем область значений функции u входит в область определения функции f.

           Тогда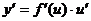 

 

           Доказательство.     

(с учетом того, что если Dx®0, то Du®0, т.к. u = g(x) – непрерывная функция)

Тогда . Теорема доказана.

Дифференциал сложной функции.

Инвариантная форма записи дифференциала.

Пусть y = f(x), x = g(t), т.е у- сложная функция.

 

Тогда dy = f¢(x)g¢(t)dt = f¢(x)dx.

 

           Видно, что форма записи дифференциала dy не зависит от того, будет ли х независимой переменной или функцией какой- то другой переменной, в связи с чем эта форма записи называется инвариантной формой записи дифференциала.

 

           Однако, если х- независимая переменная, то

dx = Dx, но

если х зависит от t, то      Dх ¹ dx.

Таким образом форма записи dy = f¢(x)Dx не является инвариантной.

Правила дифференцирования. Производные основных элементарных функций. Логарифмическое дифференцирование.

Основные правила дифференцирования.

           Обозначим f(x) = u, g(x) = v - функции, дифференцируемые в точке х.

1) (u ± v)¢ = u¢ ± v¢

2) (u×v)¢ = u×v¢ + u¢×v

3) , если v ¹ 0

           Эти правила могут быть легко доказаны на основе теорем о пределах.

Производные основных элементарных функций.

1)С¢ = 0;            9)

2)(x^m)¢ = mx^m-1;   

10)

3)   

11)

4)

12)

5)                     

13)

6)

14)

7)

15)

8)

16)