Логарифмическое дифференцирование

Рассмотрим функцию .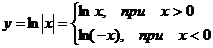

Тогда (lnïxï)¢= , т.к. .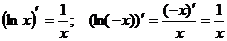

           Учитывая полученный результат, можно записать .

Отношение  называется логарифмической производной функции f(x).

           Способ логарифмического дифференцирования состоит в том, что сначала находят логарифмическую производную функции, а затем производную самой функции по формуле

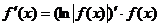
           Способ логарифмического дифференцирования удобно применять для нахождения производных сложных, особенно показательных функций, для которых непосредственное вычисление производной с использованием правил дифференцирования представляется трудоемким.

Производные и дифференциалы высших порядков. Производная параметрически заданных функций.

Производные и дифференциалы высших порядков.

           Пусть функция f(x)- дифференцируема на некотором интервале. Тогда, дифференцируя ее, получаем первую производную

           Если найти производную функции f¢(x), получим вторую производную функции f(x).

т.е. y¢¢ = (y¢)¢ или .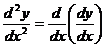

Этот процесс можно продолжить и далее, находя производные степени n.

.