Представление функций интегралами Фурье

Московский авиационный институт

(национальный исследовательский университет)

Курсовая работа

По математическому анализу

Вариант № …

                                                   Выполнил: студент гр. 30-10… С           

                                                  . ………………………………

                                              

                                                   Проверил:

                                                                 

                                                        ………………………………….

Москва 2011/12 уч. год

Часть I

 Представление функций тригонометрическими рядами Фурье

Теоретические сведения.

    1. Ортонормированная система функций.

    2. Ряд Фурье по ортонормированной системе функций.

    3. Тригонометрический ряд Фурье для 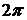- периодической функции.

    4. Достаточные условия поточечной сходимости ряда Фурье для 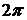- периодической функции.

    5. Тригонометрический ряд Фурье для 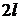- периодической функции.

    6. Тригонометрический ряд Фурье для чётной 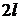- периодической функции.

    7. Тригонометрический ряд Фурье для нечётной 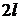- периодической функции.

    8. Комплексная форма тригонометрического ряда Фурье.

 

Практическая часть.

    1. Построить периодическое продолжение с периодом 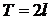 функции, заданной на отрезке 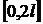. Проверить достаточные условия разложения 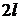- периодической функции в тригонометрический ряд Фурье. Найти коэффициенты ряда Фурье и записать разложение. Определить значения разложения в точках разрыва и на концах периодов. Построить графики исходной функции и суммы первых пяти гармоник.

    2. Построить четное продолжение на отрезок 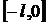  функции, заданной на отрезке 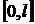. Построить периодическое продолжение с периодом  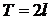функции, полученной на отрезке 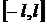. Проверить достаточные условия разложения 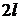- периодической функции в тригонометрический ряд Фурье. Найти коэффициенты ряда Фурье и записать разложение. Определить значения разложения в точках разрыва и на концах периодов. Построить графики исходной функции и суммы первых пяти гармоник.

    3. Построить четное продолжение на отрезок 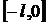  функции, заданной на отрезке 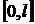. Построить периодическое продолжение с периодом  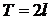функции, полученной на отрезке 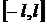. Проверить достаточные условия разложения 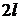- периодической функции в тригонометрический ряд Фурье. Найти коэффициенты ряда Фурье и записать разложение. Определить значения разложения в точках разрыва и на концах периодов. Построить графики исходной функции и суммы первых пяти гармоник.

 

   

Часть II

Представление функций интегралами Фурье

Теоретические сведения.

    1. Представление функции интегралом Фурье.

    2. Прямое и обратное преобразование Фурье функции.

    3. Достаточные условия представления функции интегралом Фурье.     4. Представление чётной функции интегралом Фурье.

    5. Представление нечётной функции интегралом Фурье.

    6. Комплексная форма прямого и обратного преобразования Фурье.  

Практическая часть.

    1. Построить продолжение функции, заданной на отрезке 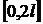, на всю числовую ось, доопределив ее нулевыми значениями вне заданного отрезка. Проверить достаточные условия представления функции интегралом Фурье. Найти прямое и обратное преобразование Фурье полученной функции. Определить значения преобразования в точках разрыва и на концах отрезка. Построить графики исходной функции и интеграла Фурье.

    2. Построить четное продолжение на отрезок 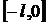  функции, заданной на отрезке 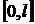. Построить продолжение функции, полученной на отрезке 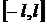, на всю числовую ось, доопределив ее нулевыми значениями вне отрезка 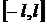. Проверить достаточные условия представления функции интегралом Фурье. Найти прямое и обратное преобразование Фурье полученной функции. Определить значения преобразования в точках разрыва и на концах отрезка. Построить графики исходной функции и интеграла Фурье.

    3. Построить нечетное продолжение на отрезок 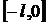  функции, заданной на отрезке 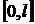. Построить продолжение функции, полученной на отрезке 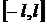, на всю числовую ось, доопределив ее нулевыми значениями вне отрезка 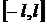. Проверить достаточные условия представления функции интегралом Фурье. Найти прямое и обратное преобразование Фурье полученной функции. Определить значения преобразования в точках разрыва и на концах отрезка. Построить графики исходной функции и интеграла Фурье.