Кинетическая энергия. Работа и мощность

8 9 10 11 12 13 14

Уравнение движения тела под действием внешней силы имеет вид (рис. 5.1)

или, в проекции на направление движения,

(5.1.1)

Рис. 5.1

Умножив обе части равенства (5.1.1) на , получим

Левая часть равенства есть полный дифференциал некоторой функции:

Если система замкнута, то и F _τ = 0. Тогда и
Если полный дифференциал некоторой функции, описывающей поведение системы, равен нулю, то эта функция может служить характеристикой состояния данной системы.
Функция состояния системы, определяемая только скоростью ее движения, называется кинетической энергией.

(5.1.2)

Кинетическая энергия системы есть функция состояния движения этой системы. K – аддитивная величина:

K – относительная величина, её значение зависит от выбора системы координат (так же как и – относительная величина).

Энергия измеряется в СИ в единицах произведения силы на расстояние, т.е. в ньютонах на метр. 1 Н·м = 1 Дж.
Кроме того, в качестве единицы измерения энергии используется внесистемная единица – электрон-вольт (эВ). 1 эВ = 1,6·10¹⁹ Дж.

При решении задач полезна формула, связывающая кинетическую энергию с импульсом p. Получим её:

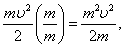
отсюда

(5.1.3)

Теперь рассмотрим связь кинетической энергии с работой.
Если постоянная сила действует на тело, то оно будет двигаться в направлении силы. Тогда элементарная работа по перемещению тела из точки 1 в точку 2, будет равна произведению силы F на перемещение dr:

dA = F d r, отсюда ,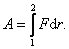
,

Окончательно получаем:

Следовательно, работа силы, приложенной к телу на пути r, численно равна изменению кинетической энергии этого тела:

(5.1.4)

Или изменение кинетической энергии dK равно работе внешних сил:

dK = dA.

Работа, так же как и кинетическая энергия, измеряется в джоулях. Скорость совершения работы (передачи энергии) называется мощность. Мощность есть работа, совершаемая в единицу времени. Мгновенная мощность , или Средняя мощность